rozwiąż algebraicznie układ równań cmods: rozwiąż algebraicznie układ równań i podaj jego interpretację graficzną w układzie współrzędnych (x=7)2+(y+4)2=49 (x−5)2+(y−1)2=36 Bardzo proszę o pomoc

Saizou : Podpowiedź: (x−a)² + (y−b)² = r² jest to równanie okręgu o środku S=(a, b) i promieniu r

Chińska podróba 6-latka: odejmij równania stronami to dostaniesz zależność liniową między x i y , następnie podstaw ją do któregokolwiek z nich

cmods: Próbowałam zrobić to przez współczynniki i wyszło mi że 24x+10y=−26 oraz jedno równanie x2−10x+y2−2y=10 Da się coś z tym zrobić?

Chińska podróba 6-latka: musisz na końcu dostać równanie już tylko z jedną niewiadomą , wszystko powiedziałem jak

6latek: (x+7)²−(x−5)²+(y+4)²−(y−1)²=13 Po przeksztalceniach i redukcji jest 24x+10y=−26 stad 10y=−26−24x y=−2,6−2,4x ============= Wstawiam do 2 rownania (x−5)²+(y−1)²=36 (x−5)²+(−2,6−2,4x−1)²=36

	18		12
(x−5)2+(−		−		x)2=36
	5		5

Po obliczeniach wychodzi

	7
x=−
	13

	13		12		7		169		84		85		17
stad y=−		−		*(−		= −		+		= −		= −
	5		5		13		65		65		65		13

	−17
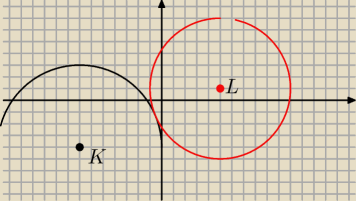
Wychodzi na to ze te okregi beda styczne i punkt stycznosci to P=(−7}{13}.		)
	13

Piersze rownanie przedstawia okrag o srodku K=(−7,−4) i r=7 Drugie rownanie przedstawia okrag o srodku L=(5,1) i r=6