| 1 | ||
oblicza ja ze wzoru ma= | √2b2+2c2−a2, gdzie a jest bokiem, na który opada środkowa | |
| 2 |

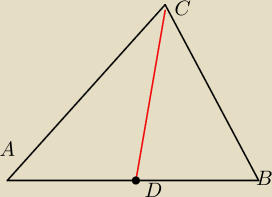 W drugiej klasie bede mial takie twierdzenie do udowodnienia
Twierdzenie : (pierwsze twierdzenia o srodkowej )
Suma kawdratow dwoch bokow trojkata jest rowna sumie podwojonego kwadratu polowy trzeciego
boku i podwojonego kwadratu srodkowej wzgledem tego boku
D∊AB AD=DB
Teza CA2+CB2= 2AD2+2DC2
Stad mozna tez obliczy dlugosc srodkowej
W drugiej klasie bede mial takie twierdzenie do udowodnienia
Twierdzenie : (pierwsze twierdzenia o srodkowej )
Suma kawdratow dwoch bokow trojkata jest rowna sumie podwojonego kwadratu polowy trzeciego
boku i podwojonego kwadratu srodkowej wzgledem tego boku
D∊AB AD=DB
Teza CA2+CB2= 2AD2+2DC2
Stad mozna tez obliczy dlugosc srodkowej
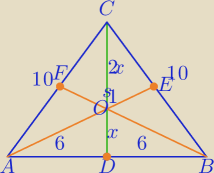 1) s1=8 z tw. Pitagorasa
2)
środkowe przecinają się w jednym punkcie i dzielą w stosunku 2:1 licząć od wierzchołka
3x=8
1) s1=8 z tw. Pitagorasa
2)
środkowe przecinają się w jednym punkcie i dzielą w stosunku 2:1 licząć od wierzchołka
3x=8
| 8 | ||
x= | ||
| 3 |
| 8 | 388 | |||
( | )2+36=|OB|2⇔|OB|2= | |||
| 3 | 9 |
| 2√97 | ||
|OB|= | ||
| 3 |
| 2√97 | √97 | |||
|FB|= | + | |||
| 3 | 3 |
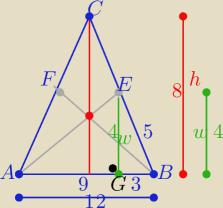 Dorzucę jeszcze taki sposób
długość środkowej na podstawę AB to h=8
P(ΔABC)=48
P(ABE)=24= 6w ⇒ w=4 to |GB|=3 to |AG|=9
|AE|=|BF|=√92+42 = √97
===================
Dorzucę jeszcze taki sposób
długość środkowej na podstawę AB to h=8
P(ΔABC)=48
P(ABE)=24= 6w ⇒ w=4 to |GB|=3 to |AG|=9
|AE|=|BF|=√92+42 = √97
===================

