Wyznaczanie równań stycznych matma.rozsz: Przez punkt P=(8,2) poprowadzono styczne do okręgu o równaniu x²+y²−2x−2y−23=0. Wyznacz równania tych stycznyc.

Phil#PW: jest to okrąg o środku S(1, 1) i promieniu r=5 Równanie stycznej: y=ax+b∊P(8,2) 2=8a+b b=2−8a y=(x−8)a+2 (x≠8) Teraz, wstawiasz to do równania okręgu (x−1)²+(y−1)²=25 (x−1)²+(ax+2−8a−1)²=25, i szukasz dla jakiego a, Δ=0

6latek: Rownanie okregu ma postac (x−1)²+(y−1)²=25 Rysujesz okrag o srodku S=(1,1) i pronieniu r=5 zaznacza w ukladzie punkt P Teraz aby wyznaczyc rownanie stycznych 1) szukana styczna ma postac y=m(x−8)+2 czyli y=mx−8m+2 Postac ogolna to y−mx+8m−2=0 Odleglosc punktu S=(1,1) od tej prostej jest rowny promieniowi r Stad wyliczysz m

6latek: Masz dwa sposoby na rozwiazanie tego zadania

Phil#PW: tak, jednak chyba Twój będzie szybszy, ze względu na to, iż u mnie mamy (a+b+c)² co niektórym może sprawić spory kłopot + potem grupowanie wyrazów podobnych

6latek: Proponuje jednak zeby zrobil tymi dwoma sposobami

matma.rozsz: czy moglibyście podać jakie powinny wyjść wyniki jak próbuję deltę to wychodzą mi same wysokie wyniki:. Z góry dzięki wielkie i również za naprowadzenie

ICSP: równanie stycznej: Ax + By + C = 0 Po podstawieniu współrzędnych punktu: C = −8A − 2B i po podstawieniu do równania stycznej: Ax + By − 8A − 2B = 0 Okrąg: S(1,1) , r = 5 Odległość stycznych od okręgu musi być równa promieniowi:

	|A + B − 8A −2B|
5 =
	√A2 + B2

wystarczy rozwiązać powyższe równanie (wyrazić A poprzez B lub na odwrót) i następnie podstawić otrzymane wartości do równania stycznej.

matma.rozsz: ICSP i właśnie tutaj jak podstawiam do równania następnie mnożę razy mianownik, aby pozbyć się ułamka i na koniec podnoszę do kwadratu obiema stronami, aby pozbyć się pierwiastka i delta wychodzi mega duża i nie wiem co robie źle.

ICSP: duża? 25(A² + B²) = 49A² + 14AB + B² 24A² + 14AB − 24B² = 0 // B = 0 ⇒ A = 0. Zakładamy B ≠ 0

	A		A
24(		)2 + 14		− 24 = 0
	B		B

	A
t =
	B

24t² + 14t − 24 = 0 12t² + 7t − 12 = 0 Δ = 625 √Δ = 25

	−7 + 25		3
t1 =		=
	24		4

	−7 − 25		4
t2 =		= −
	24		3

matma.rozsz: Oki dziękuje już wszytko jasne źle podstawiłam... Głupi błąd. WIELKIE DZIĘKI!

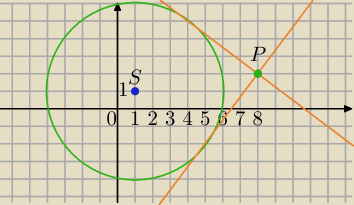
Mila: P=(8,2) 1) x²+y²−2x−2y−23=0 (x²−2x)+(y²−2y)−23=0 uzupełniamy do kwadratu dwumianu (x−1)²−1+(y−1)²−1−23 (x−1)²+(y−1)²=25 S=(1,1), r=5 2) Równanie stycznej : s: y=ax+b i P∊s⇔2=a*8+b⇔b=2−8a s: y=ax+2−8a ⇔ax−y+2−8a=0 Odległość stycznej od S jest równa 5.

	|a*1−1+2−8a|
d(S,s)=		=5
	√a2+1

|−7a+1|=5√a²+1⇔ |7a−1|=5√a²+1 /² 49a²−14a+1=25a²+25 24a²−14a−24=0 /:2 12a²−7a−12=0 Δ=49+4*144=625

	7−25		7+25
a=		lub a=
	24		24

	−18		32
a=		lub a=
	24		24

	3		3
a1=−		i s1: y=−		x+8
	4		4

========================= lub

	4		4		4
a2=		i s2: y=		x+2−8*		⇔
	3		3		3

	4		26
s2:y=		x−
	3		3

================= sprawdzaj rachunki albo odpowiedź. II sposób jest bardziej nieprzyjazny rachunkowo.

Phil#PW: a₁ i a₂ wyszły poprawnie.