Trójkąt równoboczny wpisany w okrąg
Nadia: Trójkąt równoboczny ABC jest wpisany w okrąg o promieniu 1. Na tym okręgu leży punkt P, rozny
od A,B i C. Wykaż, ze PA²+PB²+PC²=6
18 kwi 16:25
wredulus_pospolitus:
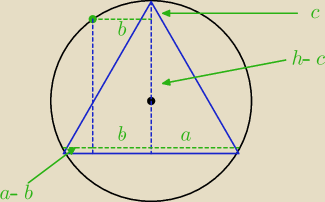
| | √3 | |
2a = √3r = √3 −−> a = |
| |
| | 2 | |
wiemy też, że: (2h/3 − c)
2 + b
2 = 1 −−−> b
2 = 1 − (2h/3 − c)
2
|PA|
2 = (a−b)
2 + (h−c)
2
|PB|
2 = (a+b)
2 + (h−c)
2
|PC|
2 = b
2 + c
2
suma = 2a
2 + 2b
2 + 2h
2 − 4hc + 2c
2 + b
2 + c
2 = 2a
2 + 2h
2 + 3b
2 + 3c
2 − 4hc =
= 2a
2 + 2h
2 + 3 − 4h
2/3 + 4hc − 3c
2 + 3c
2 − 4hc = 2a
2 + 2h
2/3 + 3 =
= 3/2 + 3/2 + 3 = 6
c.n.w.
18 kwi 16:43
och&ach:
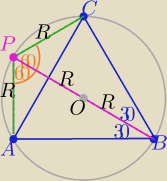
No to jeszcze tak:
Z warunku wpisania czworokąta ABCP w okrąg
|∡APC|=120
o niezależnie od wyboru punktu P≠A,B,C
zatem wartość sumy kwadratów |AP|
2+|PC|
2
też nie zależy od wyboru punktu P
można więc wybrać punkt P jako koniec średnicy BP
wtedy
|AP|
2+|PC|
2+|PB|
2= R
2+R
2+4R
2= 6R
2
dla R=1
|AP|
2+|PC|
2+|PB|
2=6
=================
co kończy dowód
18 kwi 21:30
cha&cho: 
18 kwi 21:30
och&ach:

18 kwi 21:43

 No to jeszcze tak:
Z warunku wpisania czworokąta ABCP w okrąg
|∡APC|=120o niezależnie od wyboru punktu P≠A,B,C
zatem wartość sumy kwadratów |AP|2+|PC|2
też nie zależy od wyboru punktu P
można więc wybrać punkt P jako koniec średnicy BP
wtedy
|AP|2+|PC|2+|PB|2= R2+R2+4R2= 6R2
dla R=1
|AP|2+|PC|2+|PB|2=6
=================
co kończy dowód
No to jeszcze tak:
Z warunku wpisania czworokąta ABCP w okrąg
|∡APC|=120o niezależnie od wyboru punktu P≠A,B,C
zatem wartość sumy kwadratów |AP|2+|PC|2
też nie zależy od wyboru punktu P
można więc wybrać punkt P jako koniec średnicy BP
wtedy
|AP|2+|PC|2+|PB|2= R2+R2+4R2= 6R2
dla R=1
|AP|2+|PC|2+|PB|2=6
=================
co kończy dowód

