Planimetria Zuzia: Witam Mam takie zadanie które nie do końca wiem jak obliczyć. Pomocy. W trójkąt prostokątny o przyprostokątny 5 i 12 wpisano okrąg. Oblicz pole trójkąta którego wierzchołkami są punkty styczności okręgu z bokami tego trójkąta. Obliczyłam przeciwprostokątną czyli 13. Obliczyłam pole trójkąta czyli 30. Ze wzoru na pole trójkąta P=r*p wyznaczyłam promień okręgu i wynosi on 2. Przy kacie prostym powstał kwadrat o boku 2 czyli bok szukanego trójkąta ma długość 2√2. Dodatkowo zauważyłam że kąt trójkąta który jest przy przeciwprostokątnej 13 ma miarę 45 stopni. Jak policzyć pole tego trójkąta, bo wydaje mi się że nie jest to trójkąt równoramienny. Dziękuję za każdą pomoc.

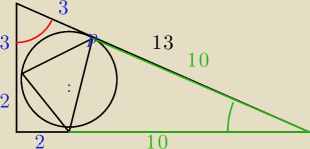
a7: ole szukanego trójkąta to pole dużego trójkata minus trzy pola małych trójkatów które trzeba odjąć od dużego

a7: P=1/2*5*12−1/2*2*2−1/2*10*10*5/13−1/2*3*3*10/13

Zuzia: Też nad tym myślałam ale jak je obliczyć skoro mam tylko ramiona? ☹️

a7: przepraszam sinus kąta między trójkami to 12/13 a nie 10/13

a7: z wzoru na pole z sinusem przeciez to trókąt prostokatny ten duży więc mamy sinusy kątów

Zuzia: Ok rozumiem czyli z sinusow kątów. Tam chyba w ostatnim powinno być 12/13

gru-gru:

	1		5
P1=		*10*10*sinα sinα=
	2		13

itd ................

Zuzia: Bardzo dziękuję 🙂

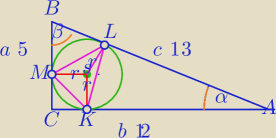
Mila: 1) W ΔACB: c=13, r=2

	5		12
sinα=		i sinβ=
	13		13

2) W ΔKLM:

	5		12
sin∡LSK=		i sin∡LSM=
	13		13

3)

	1		1		5		1		12
PΔKLM=		r2+		r2*		+		r2*		=
	2		2		13		2		13

	r2		5		12		30
=		*(1+		+		)=2*
	2		13		13		13

	60
PΔKLM=
	13