Czworokąt wpisany w okrąg Julek : Czworokąt ABCD jest wpisany w okrąg o środku O i promieniu R. Przekątne tego czworokąta są prostopadle i przecinają się w punkcie E. Udowodjij że EA²+EB²+EC²+ED²=4R²

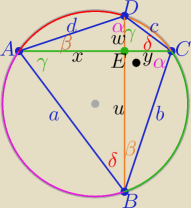
och&ach: x²+u²=a² i a²=4R²*sin²α oraz sin²α= cos²β u²+y²=b² i b²=4R²*sin²γ sin²γ= cos²δ y²+w²=c² i c²=4R²*sin²β w²+x²=d² i d²=4R²*sin²δ + −−−−−−− 2(x²+y²+w²+u²)= 4R²(cos²β+cos²δ+sin²β+sin²δ)=4R² x²+y²+w²+u²= 2R² ================ Popraw zapis w tezie zamiast 4R² ma być 2R²