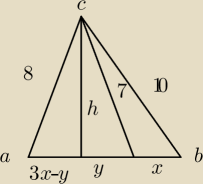
planimetria kbs: Na trójkącie ABC na boku AB obrano taki punkt D, że pole trójkąta ADC jest trzy razy większe od pola trójkąta DBC. Ponadto długość odcinka AC wynosi 8, długość odcinka CD wynosi 7 oraz długość odcinka BC to 10. Oblicz długość boku AB. dochodzę do układu trzech równań: h² + y² = 49 h² + (3x−y)² = 64 h² + (x+y)² = 100 odejmuje od 2 i 3 równania pierwsze(w tym przypadku rozpisuję nawiasy i dopiero wtedy odejmuję) : 9x² − 6xy = 15 3x² + 6xy = 153 metodą przeciwnych współczynników otrzymuję 12x² = 168 => x= √14 podstawiając pod dwa równania powyżej y wychodzi ten sam, lecz gdy z pierwszych 3 równań od 2 równania odejmę pierwsze ,a od trzeciego drugie otrzymuję : (3x−y)² − y² = 15 (x+y)² − (3x−y)² = 16 korzystam ze wzoru na różnicę kwadratu: 3x(3x−2y) = 15 4x(2y−2x) = 16 po skróceniu otrzumuję : 3x² −2xy = 5 −x² + xy =2 metodą przeciwnych współczynników otrzymuję x² = 9 => x = 3 Pomocy , nie wiem z czego wynika ,że otrzymuję różne x (sprawdzałem kilka razy obliczenia czy nie wkradł się błąd ,a równania też wydają mi się prawidłowe)

wredulus_pospolitus: 100 − 64 = 36 a nie 16

kbs: ....... dzięki sory za błąd