proszę o rozwiązanie anna: w trójkącie równobocznym ABC punkt D dzieli bok AC w taki sposób że AD : DC = 1:2 wiedząc że boki trójkąta mają długość 3 cm oblicz a) Pole trójkąta DBC b) Długość boku BD

hehe:

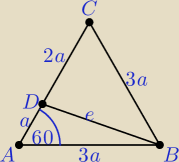
	1
3a = 3, a = 1, e z tw. cosinusów, pole ΔDBC =		*1*3*sin60o
	2

	1
albo P =		PABC
	3

eheh: Ejj .. hehe A może :

	2
P(DBC)=		P(ABC)
	3

Mila:

	9√3
PΔABC=
	4

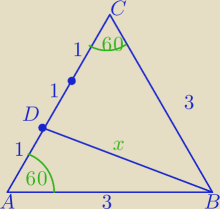
	2		9√3		3√3
a) PΔDBC=		*		=
	3		4		2

b) W ΔABD: Z tw. cosinusów x²=1²+3²−2*1*3*cos(60^o) x²=10−3=7 x=√7 [N[===]

anna: dziękuję

hehe:

	2
no pewnie że		, szkoda, że anna tego nie zauważyła
	3

eheh:

anna: zauważyłam i poprawiłam jeszcze raz dziękuję