geometria analityczna Kuba: Wyznacz równanie okręgu wpisanego w trójkąt ABC, którego wierzchołki mają współrzędne A=(−2,4) , B=(6,−4) , C=(5,3).

6latek:

	p
P=p*r stad r=
	p

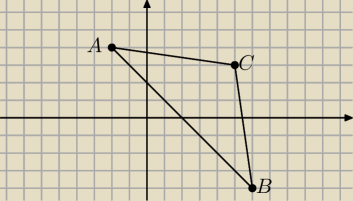
2) srodek okregu wpisanego w trojkat lezy na przcieciu sie dwusiecznych trojkata (wystarczy wyznaczyc rownania dwoch dwusiecznych i obliczyc ich punkt przciecia

6latek: sprawdzic czy ten Δ nie bedzie czasami rownoramienny jesli tak to jedna dwusieczna juz bedziesz mial (bedzie to wysokosc opuszczona z wierzcholka C na bok AB |AB|= 8√2 |AC|=√50 |BC|=√50 jest rownoramienny Teraz tylko napisz rownanie dwusiecznej kąta CAB np

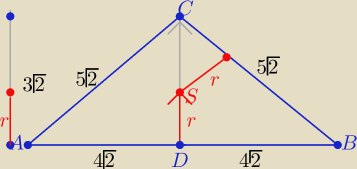
och&ach: 1/ Oblicz długości boków oraz |DC|=h P=24 Obwód L= 18√2

	24		4√2		32
to r=		⇒ r=		to r2=
	9√2		3		9

i D(2,0)

	5√2		4
|DS|=3√2−r ⇒ |DS|=		S dzieli wektor DC w stosunku k=
	3		9

	4
DS→=		DC→
	9

	4
[xS−2, yS]=		[3,3]
	9

	10		4
xS=		i yS=
	3		3

	10		4		32
o: ( x−		)2+(y−		)2=
	3		3		9

===================

och&ach: Poprawiam zapisy

	5√2
|DC|=3√2−r ⇒ |DC|=
	3