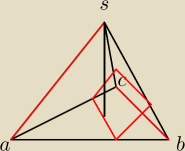
Podstawą czworościanu ABCS jest trójkąt równoramienny ABC, w którym |AB|=|AC|=a oraz 1/2a=|BC|.
Wszystkie krawędzie boczne tego ostrosłupa mają długość 2a.
Czworościan ABCS przecięto płaszczyzną, która jest równoległa do krawędzi BC i AS
oraz przechodzi przez środek okręgu opisanego na trójkącie ABC.
Oblicz pole otrzymanego przekroju.
Wiem ,że środek okregu opisanego na podstawie bedzie w spodku wysokosci
i chyba z pola moge wyliczyc ten promień.
Ale nie wiem czy to ta płaszczyzna co na rysunku (z góry przepraszam za niedokłądność,
płaszyzna w ma dochodizc do krawędzi CS)
i nie udało mi się stwierdzić nic pożytecznego co mogłoby pomóc obliczyć pole tego przekroju .
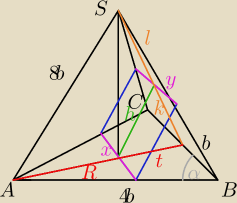U mnie tyle wszyło
Niech a = 4b.
Z tw. Pitagorasa
(R+t)2 = 16b2−b2 = 15b2
R+t = b√15
| R+t | √15 | |||
sinα = | = | |||
| 4b | 4 |
| 4b | 4b | |||||||||
2R = | = | |||||||||
| sinα |
|
| 8b | 8√15 | |||
R = | = | b | ||
| √15 | 15 |
| 8√15 | 7√15 | |||
t = b√15 − | b = | b | ||
| 15 | 15 |
| x | b | ||
= | |||
| R | R+t |
| x | b | ||||||||
= | |||||||||
| b√15 |
| 8 | ||
x = | b | |
| 15 |
| 8b | h | ||
= | |||
| R+t | t |
| 8b | h | ||||||||
= | |||||||||
| b√15 |
|
| 56 | ||
h = | b | |
| 15 |
| h | 8b | ||
= | |||
| k | l+k |
| 8b | ||||||||
= | |||||||||
| k | 3b√7 |
| 21 | ||
k = | √7b | |
| 15 |
| 21 | 24 | |||
l = 3√7b − | √7b = | √7b | ||
| 15 | 15 |
| l | l+k | ||
= | |||
| y | b |
| 3√7b | ||||||||
= | |||||||||
| y | b |
| 8 | ||
y= | b | |
| 15 |
| 1 | 56 | 8 | 8 | 56*16 | ||||||
P = | h(2x+2y) = h(x+y) = | b( | b+ | b) = | b2 | |||||
| 2 | 15 | 15 | 15 | 15*15 |
| 896 | ||
P = | b2 | |
| 225 |
| 1 | ||
Wracając z podstawieniem b = | a otrzymujemy | |
| 4 |
| 56 | ||
P = | a2 | |
| 225 |
Trochę inaczej liczyłam, ale wszystkie wielkości zgadzają się z moimi.
Ostatni rachunek poprawiłam.
