KANGUR mydlix: Ktoś umiałby rozwiązać te zadania z KANGURA 2019 − Junior? 18. Suma cyfr numeru telefonicznego postaci a a a b b b b (a≠b) jest liczbą dwucyfrową ab (cyfra dziesiątek to a, a cyfra jedności to b).Ile wynosi suma a + b? A) 8 B) 15 C) 10 D) 11 E) 12 27. W wierzchołki kwadratu wpisujemy liczby naturalne w taki sposób, że jedna z dwóch liczb wpisanych w końce dowolnego boku kwadratu dzieli drugą, żadna zaś z dwóch liczb wpisanych w końce przekątnych tego kwadratu nie dzieli drugiej. Ile wynosi możliwie najmniejsza suma czterech liczb wpisanych w wierzchołki w taki sposób? A) 12 B) 24 C) 30 D) 35 E) 60 30. Ile jest liczb czterocyfrowych, takich że po usunięciu dowolnie wybranej cyfry z jej zapisu dziesiętnego otrzymamy dziesiętny zapis liczby trzycyfrowej, która dzieli wyjściową liczbę czterocyfrową? A) 5 B) 9 C) 14 D) 19 E) 23

Minato: 3a+4b=10a+b 7a=3b Żeby ta równość zachodziła a=3 oraz b=7, zatem a+b=10 Szukaną liczba to 3337777. Suma cyfr 3+3+3+7+7+7+7=37

Mila:

kat666: 27. Liczby z narożników to (po obwodzie) 2, 12, 3, 18 30. 1100, 2200, 3300, 4400, 5500, 6600, 7700, 8800, 9900, 1200, 1500, 2400, 3600, 4800

mydlix: Dziękuję. A ktoś umiałby wytłumaczyć to to 27. i 30.?

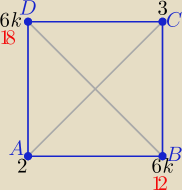
och&ach: Ustawiasz w wierzchołkach A i C dwie najmniejsze naturalne >1 takie by jedna nie dzieliła drugiej czyli 2 i 3 W wierzchołkach B i D mają dzielić i 2 i 3 więc są postaci 6k ale mają być najmniejsze i nie dzielą się nawzajem po przekątnej czyli są to 12 i 18 lub 18 i12 Najmniejsza suma takich liczb umieszczonych w wierzchołkach to 2+3+12+18 = 35 Odp: D

kat666: Ad 30: Liczba 1000a+100b+10c+d ma być podzielna przez: a) 100a+10b+c b) 100a+10b+d c) 100a+10c+d b) 100b+10b+d Warunek a) zachodzi gdy d=0 więc: Liczba 1000a+100b+10c ma być podzielna przez: b) 100a+10b c) 100a+10c b) 100b+10c Warunek b) zachodzi gdy c=0 więc: Liczba 1000a+100b ma być podzielna przez: c) 100a d) 100b co upraszcza się do: e) b jest podzielne przez a f) 10a jest podzielne przez b Wystarczy poszukać takich cyfr a,b które spełniają oba warunki