udowodnij, że (równoległobok) passata: Dany jest równoległobok ABCD oraz punkt M leżący na boku CD tego równoległoboku. Punkt M połączono z wierzchołkami A i B równoległoboku. Udowodnij, że |∡MBC|+|∡MAD|=|∡AMB|.

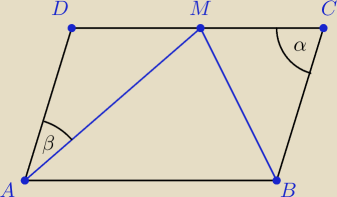
Szkolniak: Z równoległoboku wiemy, że |∡BAD|+|∡ADM|=180^o. Niech u nas |∡BAD|=α → |∡ADM|=180^o−α. Oraz niech |∡MAD|=β → |∡BAM|=α−β Kąty w ΔADM mają dać 180^o, stąd |∡AMD|=α−β Niech |∡CBM|=γ → |∡BMC|=180^o−α−γ Kąt przy wierzchołku B równy jest 180^o−α, zatem |∡ABM|=180^o−α−γ W ΔABM suma miąr kątów ma dać 180^o, zatem |∡AMB|=β+γ Mamy rozpisane w tym momencie wszystkie kąty, więc zapisujemy jaka równość ma zajść: |∡MBC|+|∡MAD|=|∡AMB| γ+β=γ+β L=P, cnw. Dosyć ciężko tam rysować, mam nadzieję że taki opis słowny będzie zrozumiały.

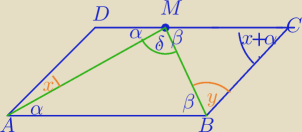Mila: Teraz licz sumy kątów w trójkatach.

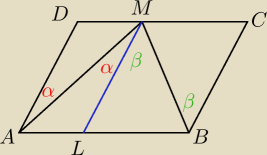Saizou : ML jest równoległa do AD i BC

Mila: Ad. 21:01 α+β+δ=180⇔δ=180−(α+β) y+β+x+α=180 x+y=180−(α+β) x+y=δ ======