rozwiąż nierówność -x^3+x^2+x-1≥0
s: Kiełbasa 1.25. i)
rozwiąż nierówność −x
3+x
2+x−1≥0
podzieliłam na x
2(x−1)(x−1) dałam przed nawias (x−1)(x
2+1) rozpisałam drugą część
(x−1)(x+1)(x−1) i wynik to −1 i 1
i jak zrobić z tego, żeby wynik wyszedł <−
∞,−1> ∨ {1}

Proszę o pomoc
16 kwi 09:11
6latek: Juz na starcie masz zle
x2*x=x3 a ma byc −x3 Poza tym x2+1≠x2−1
Proponuje zrobic tak
Pomnozyc obie strony nierownosci przez (−1)
wtedy zmieni sie jej zwrot
x3−x2−x+1≤0
x2(x−1)+1(x−1) ≤0
(x−1)(x2+1)≤0
x=1 pojedynczy pierwiastek i nalezy do zbioru rozwiazan
x2+1 to x∊R
Teraz rob wezyk
16 kwi 09:25
wredulus_pospolitus:
Zacznijmy od tego, że:
−x3 + x2 + x − 1 = x2(−x+1) + (x−1) = (−x2 + 1)(x−1) = −(x−1)2*(x+1) ≥ 0
i ... metoda wężyka się kłania
16 kwi 09:28
6latek:
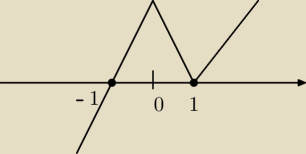
Nie patrz na to zrobilem zle . Przepraszam
poprawiam
x
3−x
2−x+1≤0
x
2(x−1)−1(x−1)≤0
(x−1)(x
2−1)≤0
(x−1)(x−1)(x+1)≤0
stad x=1 podwojny
x=−1 pojedynczy i wezyk
x∊(−
∞,−1> U{1}
16 kwi 09:33
6latek: Witam

16 kwi 09:34
s: ok, super

dziękuję Wam bardzo
16 kwi 09:56
 Proszę o pomoc
Proszę o pomoc
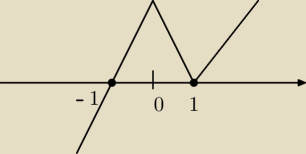 Nie patrz na to zrobilem zle . Przepraszam
poprawiam
x3−x2−x+1≤0
x2(x−1)−1(x−1)≤0
(x−1)(x2−1)≤0
(x−1)(x−1)(x+1)≤0
stad x=1 podwojny
x=−1 pojedynczy i wezyk
x∊(−∞,−1> U{1}
Nie patrz na to zrobilem zle . Przepraszam
poprawiam
x3−x2−x+1≤0
x2(x−1)−1(x−1)≤0
(x−1)(x2−1)≤0
(x−1)(x−1)(x+1)≤0
stad x=1 podwojny
x=−1 pojedynczy i wezyk
x∊(−∞,−1> U{1}

 dziękuję Wam bardzo
dziękuję Wam bardzo