maturka dzonypieczony: Wyznacz wzór funkcji g(m) , która każdej liczbie rzeczywistej przyporządkowuje najmniejszą wartość funkcji kwadratowej f(x)= x²−2mx + 3 w przedziale <0,2> . Naszkicuj wykres funkcji g(m) . dziele sobie to na 3 przyapdki i wychodzi mi tylko jeden dobrze zgodznie z kluczem odpowiedzi, byłbym wdzieczny jak by to ktoś rozwiazal bym mogl zobaczyc co robie zle

ICSP: Nie mogę Ci powiedzieć co robisz, źle jeśli nie udostępniasz swojego rozwiązania.

dzonypieczony: dobra to napisze

dzonypieczony: rozbijam na 3 przypadki: f_min=f(0) U f_min=f(2) U f_min=f(p) f_min=min{f(0)f(2)f(p)} f(0)=3 f(2)=7−4m f(p)= −m²+3 p=m jezeli mam tylko jedną wartość bez parametru to daje przypadki kiedy który przypadek będzie najmniejszy czyli dla f(0): 3≤−m²+3 U 3≤7−4m wychodzi mi część wspólna m∊(−∞;0> i w pozostałych dwoch przypadkach wychodza mi takie same przedziały a mianowicie m∊(−∞;2)U(2;∞) tylko w jednym jest jeszcze czesc wspolna z m>0 w każdym bądz razie wychodza mi zle i nei wiem jak to dokonczyc

ICSP: Jeśli x_w ∊ [0 , 2] to f_min = f(x_w) Jeśli x_w ∉ [0,2] to f_min = min{f(0) , f(2)} Czyli 1^o x_w ∊ [0,2] : 0 ≤ x_w ≤ 2

	2m
0 ≤		≤ 2
	2

0 ≤ m ≤ 1 f(x_w) = m² − 2m² + 3 = 3 − m² Dla 0 ≤ m ≤ 1 twoja funkcja jest opisana wzorem f(m) = 3 − m² 2^o x_w ∉ (0,2) Wtedy w zależności od m ∊ (−∞ ; 0) ∪ (1 ,∞) wybierasz mniejszą z liczb: f(0) = 3 f(2) = 4 − 4m + 3 = 7 − 4m Czyli jeśli f(0)< f(2) ∧ m ∊ (−∞ ; 0) ∪ (1 ,∞) wybierasz 3 Natomiast jeśli f(2) < f(0) ∧ m ∊ (−∞ ; 0) ∪ (1 ,∞) wybierasz 7 − 4m

dzonypieczony: w kluczu odpowiedzi mam ze powinno byc tak 3, m∊(−∞;0) g(m)= −m²+3, m∊<0;2> −4m+7, m∊(2;∞) i ta funkcja narysowana, to ma byc odpowiedz a mi wychodzi tylko jeden wynik z tych trzech

ICSP: jutro. Dzisiaj już robię przekształcenia typu:

	2m
0 ≤		≤ 2
	2

na 0 ≤ m ≤ 1 więc nie jest dobrze.

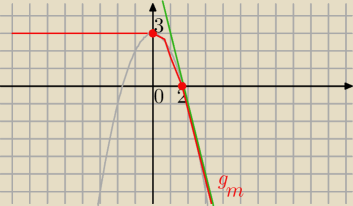
och&ach: f(x)=x²−2mx+3 w przedziale <0,2> x_w= m to f(m) = −m²+3 −− minimum dla m∊<0,1> f(0)=3 i f(2)= 7−4m jeżeli f(0)=3 −− jest minimum to f(2) >f(3) ⇔ 7−4m>3 i m∉<0,2> ⇔ m∊(−∞.0) jeżeli f(2)=7−4m −− jest minimum ⇔ 7−4m<3 i m∉<0,2> ⇔ m∊(2,∞) zatem:

	⎧	−m2+3 dla m∊<0,2>
g(m)=	⎨	3 dla m∊(−∞,0)
	⎩	7−4m dla m∊(2,∞)

och&ach: poprawiam zapis jeżeli f(0)=3 −− jest minimum to f(2) >3