Równoległobok Jam: W równoległoboku o przekątnych długości 2√3 i 2√7 jeden z boków ma długość 4. Wyznacz miarę kąta ostrego w tym równoległoboku. Może ktoś wie jak to rozwiązać i chce się podzielić?

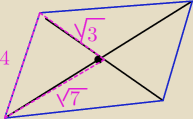
ite: Wykorzystaj to, że przekątne równoległoboku przecinają się w połowach. Dalej skorzystaj np. z tw. cosinusów dla różowego trójkąta.

chichi: α=60^o

chichi: Rozwiąż taki układ równań:

⎧	(2√3)2=42+x2−2*4*x*cos(α)
⎩	(2√7)2=42+x2+2*4*x*cos(α)	, x>0

ite: A ja opisałam szukanie miary kąta między przekątnymi równoległoboku

och&ach: W każdym równoległoboku: f²+e²=2a²+2b² zatem 28+12=2a²+32 ⇒ a=2 z tw. cosinusów

	42+22−(2√3)2
cosα=		=.......
	2*4*2

α=60^o