Równanie parametr jon: Wyznacz te wartości parametru m dla których oba rozwiązania równania mx²− ( m² +m +1)x +m +1=0 są większe od 1. Czy może mi to ktoś rozwiązać? Z góry wielkie dzięki!

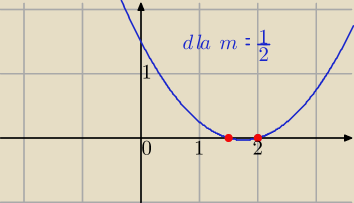
Mila: Oba rozwiązania równania mx²− ( m² +m +1)x +m +1=0 są większe od 1 f(x)=mx²− ( m² +m +1)x +m +1 m≠0 1) Δ≥0 ( m² +m +1)²−4*m(m+1) >0 (m²+m+1)²=m⁴+2m³+3m²+2m+1 Δ=m⁴+2m³+3m²+2m+1−4m²−4m=m⁴+2m³−m²−2m+1=(m²+m−1)²⇔ Δ=(m²+m−1)²≥0 dla m∊R i 2) x₁,x₂>1 m>0 parabola skierowana do góry i

	m2+m+1
f(1)>0 i		>1
	2m

f(1)=m− ( m² +m +1) +m +1=−m²+m m∊(0,1) i m²+m+1>2m⇔m²−m+1>0 dla m∊R bo Δ<0⇔ m∊(0,1) lub m<0 i Δ≥0

	m2+m+1
f(1)<0 i		>1
	2m

m<0 i m²+m+1<2m − brak rozw. =========== odp.

	−1+√5
m∊(0,1) w tym dla m=		ma pierwiastek podwójny >1
	2

Posprawdzaj rachunki, może masz odpowiedź?

321: Teoretycznie jak robiliśmy na zajęciach wyszło ze m należy do R

321: Może jon ma odpowiedzi do tego.

ICSP: Już dla m = 0 nie dostajemy dwóch rozwiązań, więc odpowiedzią nie może być m∊R