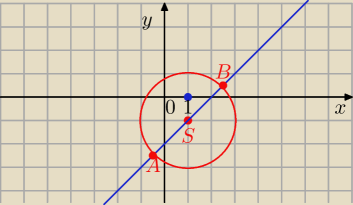
Okrąg 321: Wyznacz punkty wspólne okręgu o środku S (1,−1) i promieniu r=2 z prostą przechodzącą przez punkt S i nachyloną do osi OX pod kątem 45 stopni. Mam prośbę, czy mógłby mi ktoś wytłumaczyć jak to zrobić i rozpisać?

janek191: ( x − 1)² + ( y + 1)² = 4 tg 45^o = 1 czyli a = 1 y = x + b S = ( 1, −1) więc − 1 = 1 + b ⇒ b = −2 y = x − 2 Podstaw za y do równania okręgu ( x − 2) i oblicz iksy i igreki Otrzymamy równanie x² −2 x − 1 = 0 Δ = 8 √Δ = 2√2 x₁ = 1 − √2 x₂ = 1 + √2 y₁ = −1 − √2 y₂ = − 1 + √2

321: Bardzo dziękuję!