Zdarzenie losowe A,B są zawarte w Ω oraz P(A∩B')=0,7. Wykaż, że P(A'∩B)≤3. Kck: Zdarzenie losowe A,B są zawarte w Ω oraz P(A∩B')=0,7. Wykaż, że P(A'∩B)≤3. W jaki sposób rozwiązać to zadanie? Czy istnieje sposób w który mógłbym narysować P(A∩B') używając diagramów Venna? O wiele łatwiej rozwiązuje mi się zadania gdy mogę zobaczyć je na diagramie.

ite: Nie pomyłki w zapisie P(A'∩B)≤3 ?

Kck: Wydaje mi się, że wszystko dobrze przepisałem. Jest to zadanie z majowej matury 2012. Napiszę jeszcze raz: Zdarzenia losowe A,B są zawarte w Ω oraz P(A∩B')=0.7 (A' oznacza zdarzenie przeciwne do zdarzenia A, B' oznacza zdarzenie przeciwne do zdarzenia B). Wykaż, że P(A'∩B)≤3.))

Chińska podróba 6-latka: źle przepisało, zadanie byłoby trywialne , tam powinno być 0,3

ite: Z definicji wartość prawdopodobieństwa należy do przedziału [0,1], więc jest mniejsza od 3. Może miało być 0,3 ?

Chińska podróba 6-latka: tak właśnie miało być , i wtedy na plackach zbiorów to widać od razu

ite: Te placki do chińskiej zupy?

Chińska podróba 6-latka: takie placki https://pl.wikipedia.org/wiki/Diagram_Venna

Kck: Faktycznie, dwa razy źle przepisałem. Czyli jak na diagramach wyglądałoby rozwiązanie tego zadania?

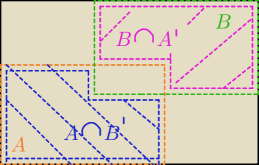
ite: Jedna z możliwości wyglądałaby np. tak ↑ (wizja kubistyczna, nieplackowa) Obszary granatowy (0,7 całego obszaru) i różowy są rozłączne. Różowy może więc zająć co najwyżej pozostałe pole czyli nie więcej niż 1−0,7.