proszę o rozwiązanie anna: Punkt S = (− 1,5) jest środkiem okręgu wpisanego w trójkąt ABC , w którym A = (− 16,− 10 ) i B = (8,− 2) . Oblicz pole koła wpisanego w trójkąt ABC .

suchaszosa: Wyznacz odległość punktu S o prostej AB

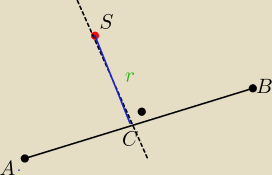
6latek: Zrob rysunek do zadania 1) SC=r to promien okregu wpisanego 2) Piszesz rownanie prostej AB −potem przeksztalc ja do postaci ogolnej 2) Odleglosc punktu S o prostej AB to wlasnie promien r tego okregu Masz na to wzor Pole kola wpisanego P=πr²

och&ach: P_k=90π

chichi: Rysunek z 22:22 jakim cudem ten okrąg będzie wpisany w trójkąt, jeśli ten trójkąt nawet nie powstanie gdyż punkty A, B i C są współliniowe?

6latek: Niech poprawi zamiast C na D i bedzie gitara

anna: dziękuję zadanie już rozwiązałam P_k = 90 π