Całka Fineasz: Mam do policzenia objętość figury korzystając z całki podwójnej. Bryła jest ograniczona dwiema płaszczyznami x+2y+z=−1, x+2y−2=0 oraz płaszczyznami układu współrzędnych Wykonałem rysunek w 3d, jednak ciężko mi odczytać obszar całkowania. ∫∫−x−2y−2dydx. Pytanie jaki oznaczyć te całki?

Fineasz: x+2y+z=−2*

jc: Odbiłem względem zera (minusy zostawiam wielbicielom liczb ujemnych. x+2y+z=1 x=2y+z=2 x=0 y=0 z=0 Pierwsza płaszczyzna wycina czworościan o wierzchołkach: (0,0,0), (1,0,0), (0,1/2,0), (0,0,1) i objętości = 1/12 Druga wycina dwa razy większy czworościan. Różnica objętości = 1/12.

jc: Oj, dwa razy większy, więc o objętości 8 razy większej. Różnica objętości = 8/12 − 1/12 = 7/12

Fineasz:

	10
W odpowiedziach mam		, A można poprosić o pomoc jak to zrobić całką podwójną?
	3

jc: Jaki obszar masz na myśli? x≥0, y≥0, z≥0, 1 ≤ x+2y+z ≤ 2, czy jakiś inny? (u Ciebie: x≤0, y≤0, z≤0, −2 ≤ x+2y+z ≤ −1)

luui: V = _D∫∫ x+2y+2 dydx D: 0≤x≤2

	−x
0≤y≤		+1
	2

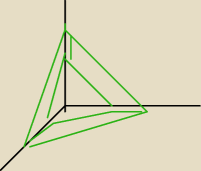
jc: Bryła to czworościan ścięty.

Fineasz: Nawiązując do 21:43 licząc całkę po dy wychodzi mi xy+y²+2y I ^−1/2x+1 0 −x +3 ∫−x+3dx −1/2x²+3x I² 0 =4

luui: https://www.wolframalpha.com/input/?i=integral+%28+x%2B2y%2B2+dy+dx%29++from+0+to+%28-x%2F2%2B1%29%2C+from+0+to+2

Fineasz: Dzięki wielkie

jc: Poprawiłem drugą płaszczyznę, a autor pomylił pierwszą.