Pole figur płaskich Michał: Okrąg wpisany w trójkąt ma promień o długości 5. Punkt styczności dzieli jeden z boków na odcinki o długości 8 i 12. Oblicz pole tego trójkąta. Mam pomysł na to zadanie, ale nie jestem pewien. Czy obwód tego trójkąta wynosi 50?

Szkolniak:

	9600
mi pole wyszło		, ale nie wiem czy dobrze
	71

chichi: @Szkolniak jest okej

Jerzy: Tutaj masz podobne zadanie: https://zadania.info/d502/1869408

Michał: dziękuję za to zadanie podobne

Michał: Dziękuje za pomoc, wyszło mi tyle samo

kerajs: Dorzucę trzecią wersję.

	5		5
Niech kątami trójkąta będą: 2α, 2β, 2γ takie, że tg α=		i tg β=
	8		12

	tg α+tg β
ctg γ=ctg (90o−α−β)=tg (α+β)=		=
	1−tg α tg β

	5   5   + 8   12		100
=		=
	5   5   1− *   8   12		71

x
	=ctg γ
5

	500
x=
	71

	500
P=(a+b+c)r=(8+12+		)*5
	71

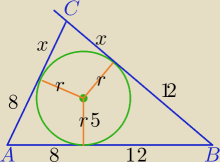
Mila: p=20+x− połowa obwodu Δ P_Δ=(20+x)*5 P_Δ=√(20+x)*8*x*12 /² (20+x)*96x=25*(20+x)² 96x=25(x+20) 71x=500

	500
x=
	71

	2500
PΔ=(20+x)*5=100+
	71

	9600
PΔ=
	71

==========

6latek: Dobry wieczor Milu Trzecia linijka od gory (wzor na pole trojkata ) to wzor Herona ?

chichi: Nie możesz sam sprawdzić?

6latek: Moge ale chcialem sie przywitać

Mila: Witam Tak wzór Herona. Czytałam wczoraj i wnioskuję, że już zdrowy jesteś

6latek: NIe calkiem tak na tip top ale znacznie lepiej . Milu natomiast janek191 odpisal dzisiaj i nadal jest na kwarantannie i czuje sie srednio .Ma odpisac kiedy poczuje sie znacznie lepiej

Mila: Pozdrów Janka, gdy do niego napiszesz. Zdrowiej

6latek: Zrobię to . Dziękuje i dobranoc

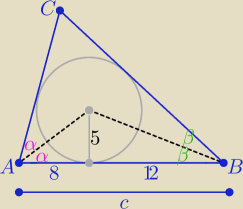
figa: Dorzucę jeszcze taki sposób

	1		c2
P(ABC)=		*
	2		ctg2α+ctg2β

=========================

	5		2tgα
tgα=		to tg2α=
	8		1−tg2α

	80		39
tg2α=		, ctg2α=
	39		80

	5		120		119
tgβ=		to tg2β=		, ctg2β=
	12		119		120

c²=400 ........................

	9600
P==
	71

=============