Pomoże ktoś pilne
Smito: 1.49 Określ, dla jakich wartości współczynników a, b i c do wykresu funkcji kwadratowej
gdzie f(x)=ax2 + bx + c należą punkty A i B gdy
f(x) = ax2 + x +c A = (−2,−3) i B = (3,−3)
14 kwi 12:38
Chińska podróba 6-latka: | | 1 | |
skoro dla −2 i 3 jest taka sama wartość −3, to wierzchołek ma pierwszą współrzędną |
| |
| | 2 | |
14 kwi 12:43
janek191:
f(x) = a x2 + x + c więc b = 1
A =( −2, −3)
więc mamy
a*(−2)2 −2 + c = −3
4a −2 + c = −3
B = ( 3, −3)
więc mamy
a*32 + 3 + c = −3
9a + 3 + c = −3
Zatem mamy układ równań
4a + c = −1
9a + c = − 6
−−−−−−−−−−−−−−−−−−−− odejmujemy stronami
( 9a + c) − ( 4a + c) = − 6 − ( −1)
5 a = − 5 / : 5
a = − 1
=====
Wstawiam −1 za a do równania 4a + c = −1
Mamy
−4 + c = − 1
c = −1 + 4 = 3
===============
Odp.
a = −1, b = 1, c = 3
14 kwi 13:03
janek191:
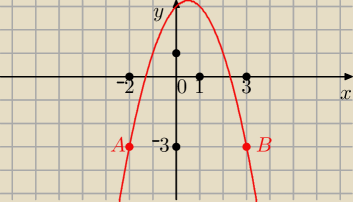
14 kwi 13:10
IXXMM:
f(x)=ax2+x+c A(−2,−3) , B(3, −3) , b=1
f(−2)=f(3) ⇒ 4a−2=9a+3 ⇒ a= −1
f(−2)=−1 ⇒ −4−2+c=−3 ⇒ c=3
a=−1,b=1 , c=3
14 kwi 13:31
MMXXI: 
14 kwi 14:54
IXXMM:

14 kwi 15:01


