| 1 | ||
równaniach: y=2x−1, y=2x+3, y=− | x | |
| 2 |
| 4 | ||
obliczyłem r= | próbowałem zrobić układ równań ale nie znam żadnej współrzędnej i mam 2 | |
| √5 |
| |3−(−1)| | 4 | |||
odleglosc miedzy tymi prostymi rownoleglymi d= | = | |||
| √4+1 | √5 |
| 2 | ||
Ale to bedzie srednica okregu wiec r= | ||
| √5 |
| 1 | ||
Zauwaz tez ze prosta y=− | x jest prostopadla zarowno jak do prostej y=2x−1 i y=2x+3 | |
| 2 |
| 1 | ||
y=− | x wynosi r | |
| 2 |
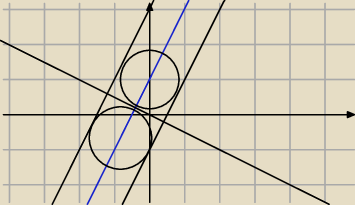 Jak widzisz środek takich okręgów leży na niebieskiej prostej.
Promień okręgu znasz, więc dokładne współrzędne środka wyliczysz z wzoru na odległość punktu
(środka) od proste x + 2y = 0
Jak widzisz środek takich okręgów leży na niebieskiej prostej.
Promień okręgu znasz, więc dokładne współrzędne środka wyliczysz z wzoru na odległość punktu
(środka) od proste x + 2y = 0
| 2 | 1 | |||
SAB=(− | , | ) | ||
| 5 | 5 |
| 1 | ||
O(x,2x+1) y=− | x | |
| 2 |
| 4 | 3 | |||
S1(0,1) S2(− | ,− | ) | ||
| 5 | 5 |
| 4 | ||
1. x2+(y−1)2= | ||
| 5 |
| 4 | 3 | 4 | ||||
2. (x+ | )2+(y+ | )2= | ||||
| 5 | 5 | 5 |
