Trójkąt, pole Szkolniak: Oblicz pole trójkąta o bokach długości √5, √13 i √26. Można to Heronem, ale to katorga, w takim razie spróbowałem inaczej i wyszło mi pole równe

	7
		. Byłbym bardzo wdzięczny gdyby ktoś potwierdził czy jest ok?
	2

Maciess: https://www.wolframalpha.com/input/?i=sqrt(p(p-sqrt(13))(p-sqrt(5))(p-sqrt(26)))+,+where+p=(sqrt(5)+sqrt(13)+sqrt(26))/2

Szkolniak: Super, wychodzi tyle samo, dziękuję!

wredulus_pospolitus: yep, jest dobrze. z tw. cosinusa robiłeś i później pole przy pomocy sinusa ? @Maciess −−− zapomniałeś o '+'

chichi: To dobry traf

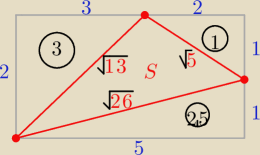
blabla: S= 10(−3+1+2,5) S=3,5 =====

blabla: Poprawiam zapis S=10−(3+1+2,5)

chichi: Super @blabla Posiłkując się twoim rozwiązaniem można też tak: A=(0,0) B=(5,1) C=(3,2)

	1		7
vec(AB)=[5,1] ∧ vec(BC)=[3,2] ⇒ P=		(5*2−3*1)=
	2		2

blabla: Moje bez obliczeń

6latek: Pytanie Jak rozwiazanie blabla byloby ocenione na maturze ? Jest łatwe i przyjemne

chichi: @blabla otóż to @6latek też jestem ciekaw, ale dla mnie max punktów

Szkolniak: wredulus nie nie, najpierw z tw. cosinusów, potem wysokość wyznaczyłem i ze wzoru P=a*h.

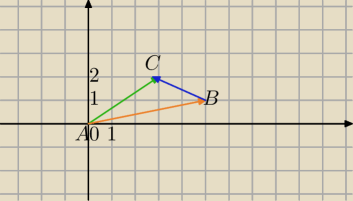
trop: W układzie wsp. 13=3²+2² wektor AC=[3,2] ma długość √13 26=5²+1² wektor AB=[5,1] ma długość √26 5=2²+1² wektor BC= [−2,1] ma dł.√5 ================= 3 2 5 1

	1		7
PΔ=		*|3−10|=
	2		2

port:

hot dog: Hej port, tym razem pudło, to nie ja

dalmatyńczyk: