Próbna matiura OPERON 2020 Marzec Już za miesiąc: Punkty A= (1,3) i B = (7,5) są kolejnymi wierzchołkami rombu ABCD, przy czym punkt A jest wierzchołkiem kąta rozwartego tego rombu. Wierzchołki C i D leżą na prostej danej równaniem x−3y−8=0. Wyznacz współrzędne wierzchołków C i D oraz równanie okręgu wpisanego w ten romb. Próbuje wyznaczyć jeden z wierzchołków na podstawie tego żę |AB|=|AD| ale ciągle wychodzą mi dwa rozwiązania z czego jedno jest dobre a drugie złe i nie mogę znaleźć błędu.

wredulus_pospolitus: co z tym równaniem okręgu

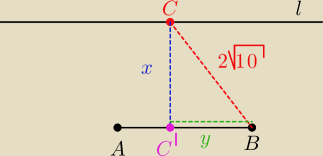
wredulus_pospolitus: x −−− odległość pomiędzy prostą l i odcinkiem AB y −−− szukana odległość −−−> z niej masz punkt C^l z którego później masz C ... D to już wtedy banał

Już za miesiąc: |AB|²=40 |AB|²=|AD|² 40=(x−1)² + (1/3x −8/3−3)² 40=x²−2x+1+1/9x²−34/9x+ 289/9 /*9 360=10x² − 52x + 298 10x²−52x−62=0 5x²−26x−31=0 Δ=676+620=1296 √Δ=36 x₁=(26−36)/10=−1 x₂=(26+36)/10= 6,2 no i ta odpowiedź jest zła i nie wiem co źle liczę tutaj. Tutaj jest klucz https://arkusze.gieldamaturalna.pl/uploads/6b9cdf9e5837489566a804abf872a9c09f81313e.pdf

wredulus_pospolitus: dobrze liczysz ... po prostu musisz odrzucić x₂ ... ponieważ .... jest podane, że przy wierzchołku A masz kąt rozwarty

Już za miesiąc: Tylko właśnie dlaczego to że tam jest kąt rozwarty mogę odrzucić drugie rozwiązanie ?

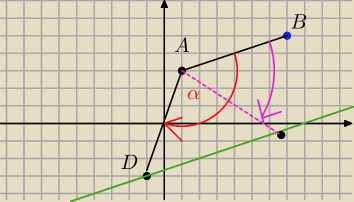
6latek: Gdybys zrobil rysunek do zadania od razu zauwazylbys ze dla punktu D ktory bedzie mial

	1		8
wspolrzedna x=−1 i y=		x−		=−3
	3		3

jest kąt rozwarty Zauwaz ze jesli punkt D mialby wspolrzedna x=−6,2 tak ja policzyles −policz wspolrzedna y i zaznacz na prostej ten punkt i zobaczysz ze wtedy masz kąt ostry a nierozwarty jak w tresci zadania

6latek: Rownanie okregu wpisanego 1) wyznacz srodek odcinka DB gdyz przekatna rombu jest jego dwusieczna i masz wspolrzedne srodka okregu wpisanego 2) Obliczenie promienia P=p*r gdzie R −pole czworokata , p− polowa obwodu

	2P
stad r=
	4a

Pamietaj z e w rownaniu okregu promien r jest do potegi drugiej