proszę o rozwiązanie
anna: Punkt P należy do okręgu opisanego na prostokącie ABCD .
Wykaż, że |PA |2 + |P C| 2= |P B|2 + |P D |2 .
PIC
13 kwi 10:37
wredulus_pospolitus:
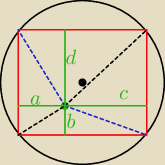
zauważ, że:
|PA|
2 = a
2 + b
2
|PB|
2 = b
2 + c
2
|PC|
2 = c
2 + d
2
|PD|
2 = d
2 + a
2
teraz samodzielnie rozpatrz (będzie bardzo podobnie) co jeżeli punkt P leży wewnątrz okręgu,
ale leży poza prostokątem
13 kwi 10:42
chichi:
Punkt leżący wewnątrz okręgu do niego nie należy, nawet środek okregu nie należy do okręgu. Do
zadania oryginalnie jest rysunek z zaznaczonym punktem P

13 kwi 10:53
wredulus_pospolitus:
Ach ... okręg ... a ja myślałem sobie o kole.
No ale idea rozwiązania dokładnie taka sama
13 kwi 10:55
Mila:
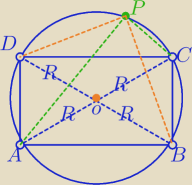
Wykaż, że |PA |
2 + |P C|
2= |P B|
2 + |P D |
2
∡APC=90
o jako wpisany oparty na średnicy AC.
|AP|
2+|PC|
2=|AC|
2
∡BPD=90
o jako wpisany oparty na średnicy BD.
|PB|
2+|PD|
2=|BD|
2
⇔
|PA |
2 + |P C|
2= |P B|
2 + |P D |
2
13 kwi 21:15
anna: dziękuję
14 kwi 06:52
 zauważ, że:
|PA|2 = a2 + b2
|PB|2 = b2 + c2
|PC|2 = c2 + d2
|PD|2 = d2 + a2
teraz samodzielnie rozpatrz (będzie bardzo podobnie) co jeżeli punkt P leży wewnątrz okręgu,
ale leży poza prostokątem
zauważ, że:
|PA|2 = a2 + b2
|PB|2 = b2 + c2
|PC|2 = c2 + d2
|PD|2 = d2 + a2
teraz samodzielnie rozpatrz (będzie bardzo podobnie) co jeżeli punkt P leży wewnątrz okręgu,
ale leży poza prostokątem

 Wykaż, że |PA |2 + |P C| 2= |P B|2 + |P D |2
∡APC=90o jako wpisany oparty na średnicy AC.
|AP|2+|PC|2=|AC|2
∡BPD=90o jako wpisany oparty na średnicy BD.
|PB|2+|PD|2=|BD|2
⇔
|PA |2 + |P C| 2= |P B|2 + |P D |2
Wykaż, że |PA |2 + |P C| 2= |P B|2 + |P D |2
∡APC=90o jako wpisany oparty na średnicy AC.
|AP|2+|PC|2=|AC|2
∡BPD=90o jako wpisany oparty na średnicy BD.
|PB|2+|PD|2=|BD|2
⇔
|PA |2 + |P C| 2= |P B|2 + |P D |2