geometria analityczna DAniel: Wyznacz równanie zbioru środków wszystkich cięciw okręgu (x−4)² + (y−1)² = 25 przechodzących przez punkt P(0,1)

I'm back: Na jakim poziomie nauczania jesteś? W ramach czego masz to zadanie?

DAniel: Jestem w 3 klasie liceum i przygotowuję się do konkursu− jest to zadnie z jakiegoś starszego zbioru przygotowującego do matury.

wredulus_pospolitus: Okey ... to skoro jest to przygotowanie na konkurs to pytania mam: 1) Jakieś pomysły? 2) Jakieś domysły? 3) Jakie są współrzędne dwóch punktów które 'na start' możesz podać? Jeśli to było ze starego zbioru do matury, to musiało to być z bardzo starego i raczej było to zadanie na '6'.

DAniel: Wyznaczyć równanie prostej y=ax+3−3a, potem to wstawić do równania okręgu i wychodzi równanie kwadrow (a² +1)x² + (6a−6a² −12)x + 9a² −18a−5=0 i potem wyznaczyć sumę rozwiązań i się pojawia problem z dokończeniem bo nie wiem jak to dalej zrobić.

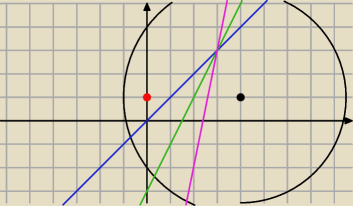
wredulus_pospolitus: Co reprezentuje sobą rodzina prostych y = ax + 3 − 3a Przecież one nawet nie przechodzą (po za jedną) przez punkt P(0,1). No ale nawet przy założeniu, że poprawisz równanie tej rodziny prostych, co daje Ci podstawienie ich wzoru do równania okręgu? Odpowiedź: Daje Ci równanie kwadratowe (z parametrem 'a') którego rozwiązaniami są współrzędne x'owe przecięcia się danej prostej z okręgiem. Więc co dalej −−− dalej robisz średnią arytmetyczną rozwiązań tegoż równania i masz współrzędną x'ową (zależną od 'a') środka tejże cięciwy. Wstawiasz do równania prostej i masz drugą współrzędną. W teorii − jest to do wyliczenia i przy wykorzystaniu wzoru Viete'a bezboleśnie wyznaczysz

	x1 + x2
xszukana =
	2

DAniel: złą prostą napisałem po pomyliłem zadania

DAniel: prosta to y=ax+1 a równanie (1+a² )x² −8x−9=0

wredulus_pospolitus: tak więc środki cięciw będą miały współrzędne:

	4		(a+1)2
(		,		)
	a2+1		a2+1

DAniel:

	4a
A współrzędna Y nie będzie czasem
	a2 +1

wredulus_pospolitus: Poprawka

	a2 + 4a + 1
y'rekowa winna być
	a2+1

no i nadal czekam na odpowiedź na moje dwa pozostałe dwa pytania, bo szczerze mówiąc gdyby to było zadanie konkursowe to nie dostałbyś pełnej puli punktów za takie rozwiązanie

wredulus_pospolitus:

	4
x:=
	a2+1

	4a
y:=		+1
	a2+1

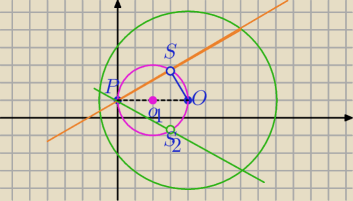
Mila: II sposób (x−4)² + (y−1)² = 25 S=(x,y) środek dowolnej cięciwy przechodzącej przez punkt P P=(0,1), O=(4,1), |OP|=4 1) ΔPSO− Δprostokątny |OP|²=|OS|²+|PS|² 4²=(x−4)²+(y−1)²+x²+(y−1)² stąd : O₁:(x−2)²+(y−1)²=4 środki cięciw przechodzących przez punkt P leżą na okręgu O₁.