proszę o rozwiązanie
anna: Dany jest romb ABCD o boku długości 26, w którym przekątna BD ma długość równą 20.
Punkt E jest środkiem boku AD (zobacz rysunek).
PIC
Oblicz sinus kąta α , jaki odcinek BE tworzy z bokiem AB rombu ABCD .
12 kwi 23:46
wredulus_pospolitus:
a gdzie jest punkt E w tym rombie

12 kwi 23:48
wredulus_pospolitus: dobra ... cofam pytanie

12 kwi 23:48
wredulus_pospolitus:
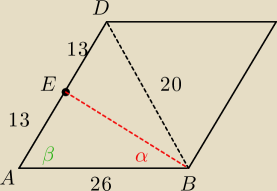
propozycja
1) z tw. cosinusów wyznaczasz wartość cosinusa kąta β patrząc na boki trójkąta ABD.
2) bierzesz tą wartość cosβ, aby wyliczyć |BE| z tw. cosinusów
3) bierzesz wartości boków trójkąta ABE do tw. cosinusów w celu wyznaczenia wartości cosα
4) wyznaczasz wartość sinα wykorzystując jedynkę trygonometryczną
12 kwi 23:52
urban:
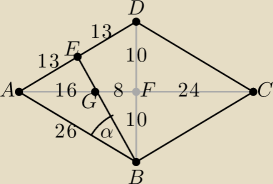
| | 1 | |
|FC| = |AF| = √ 262 − 102 = 24. Pole rombu P = |
| *20*48 = 480. |
| | 2 | |
| | 1 | |
Pola trójkątów ABE, EBD są równe |
| P = 120. |
| | 4 | |
G − środek ciężkości trójkąta ABD, dzieli środkową AF na 2 odcinki w stosunku 2:1 od strony A,
więc |AG| = 16 i |GF| = 8 oraz z tw. Pitagorasa |BG| =
√102 + 82 =
√164 = 2
√41,
| | 2 | |
|BG| = |
| |BE|, zatem |BE| = 3√41. |
| | 3 | |
| | 1 | |
Pole trójkąta ABE: |
| *26*3 √41*sinα = 120, stąd sinα =  |
| | 2 | |
13 kwi 01:22
chichi:
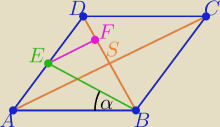
|AS|=
√676−100=24 |DF|=5 |ED|=13 |EF|=12 − trójkąt (5,12,13)
Tw. Pitagorasa w ΔBFE: |EB|=
√225+144=3
√41
| | 1 | | 1 | |
PΔABD= |
| *20*24=240= |
| PΔABE ⇒ PΔABE=120 |
| | 2 | | 2 | |
| 1 | | 40√41 | |
| *26*3√41*sin(α)=120 ⇒ sin(α)= |
| |
| 2 | | 533 | |
13 kwi 01:38
anna: przepraszam że nie narysowałam rysunku ale nie umiem tego wykonać
rysunek poprawny jest taki jak narysował chichi 13 kwi 01:38
dziękuję
13 kwi 09:47
urban:
a mój dlaczego jest niepoprawny wg Ciebie Anno?

13 kwi 10:06
anna: rysunek który jest podany w zadaniu jest taki że I BE Inie jest prostopadły do odcinka I AD I
chociaż muszę przyznać że chyba to nie ma znaczenia bo wynik jest taki sam
a to dlatego że figura to romb
jeszcze raz dziękuję
13 kwi 10:32
6latek: A sama bys zrobila rysunek do zadania ?
Odcinek BE nie moze byc prostopadly do odcinka AD nie z tego wzgledu ze to akuratnie romb
Rozpatrz trojkat ABD . Jest to trojkata rownoramienny 26,26,20
Odcinek BE jest srodkowa a nie wysokoscia (ta pada pod kątem prostym na dany bok)
Rysunek urban jak najbardziej prawidlowy
13 kwi 10:56
anna: masz rację i przepraszam wszystkich za moje niedociągnięcia i jeszcze raz dziękuję
13 kwi 11:02
urban:
Uff! Kamień z serca

13 kwi 11:14
blabla:

13 kwi 12:34
Bond:
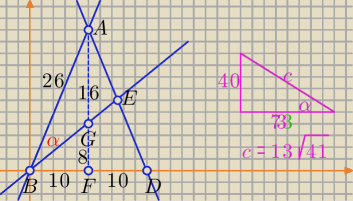
jeszcze jedno rozwiązania

|AB| = 26, |BF| = 10, |FA| = 24, G − środek ciężkości, |EG| = 8,
A (10, 24), B (0, 0), G (10, 8)
współczynniki kierunkowe prostych: AB: a
AB = 2,4, AG: a
AG = 0,8
| | 2,4 − 0,8 | | 40 | | 40 | |
tgα = | |
| | = |
| i α jest kątem ostrym, to sinα = |
| |
| | 1 + 2,4*0,8 | | 73 | | c | |
13 kwi 13:37
James Bond:

13 kwi 14:06
Bond:
dla agenta 007

13 kwi 14:08
007:

13 kwi 14:13


 propozycja
1) z tw. cosinusów wyznaczasz wartość cosinusa kąta β patrząc na boki trójkąta ABD.
2) bierzesz tą wartość cosβ, aby wyliczyć |BE| z tw. cosinusów
3) bierzesz wartości boków trójkąta ABE do tw. cosinusów w celu wyznaczenia wartości cosα
4) wyznaczasz wartość sinα wykorzystując jedynkę trygonometryczną
propozycja
1) z tw. cosinusów wyznaczasz wartość cosinusa kąta β patrząc na boki trójkąta ABD.
2) bierzesz tą wartość cosβ, aby wyliczyć |BE| z tw. cosinusów
3) bierzesz wartości boków trójkąta ABE do tw. cosinusów w celu wyznaczenia wartości cosα
4) wyznaczasz wartość sinα wykorzystując jedynkę trygonometryczną


 |AS|=√676−100=24 |DF|=5 |ED|=13 |EF|=12 − trójkąt (5,12,13)
Tw. Pitagorasa w ΔBFE: |EB|=√225+144=3√41
|AS|=√676−100=24 |DF|=5 |ED|=13 |EF|=12 − trójkąt (5,12,13)
Tw. Pitagorasa w ΔBFE: |EB|=√225+144=3√41



 jeszcze jedno rozwiązania
jeszcze jedno rozwiązania  |AB| = 26, |BF| = 10, |FA| = 24, G − środek ciężkości, |EG| = 8,
A (10, 24), B (0, 0), G (10, 8)
współczynniki kierunkowe prostych: AB: aAB = 2,4, AG: aAG = 0,8
|AB| = 26, |BF| = 10, |FA| = 24, G − środek ciężkości, |EG| = 8,
A (10, 24), B (0, 0), G (10, 8)
współczynniki kierunkowe prostych: AB: aAB = 2,4, AG: aAG = 0,8


