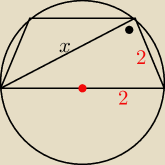
Na trapezie równoramiennym opisany jest okrąg o promieniu 2 cm. Karol: Na trapezie równoramiennym opisano okrąg, promien okregu jest równy połowie długosci dłuższej podstawy. Promień okregu i ramię trapezu są równe 2 cm. Należy obliczyć pole i długość przekątnej. Pytanie czy wynik w ksiażce jest zły (P= 27√3/4 i x=3√3), czy ja źle zakładam że okrąg jest opisany także na trójkącie prostokątnym i z tego liczę przekątną z pitagorasa. Moje wyniki to P=3√3 i x=2√3.

chichi: Przepisz dokładnie polecenie z książki, nie swoimi słowami

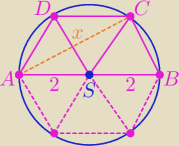chichi: Jeśli polecenie jest takie jak piszesz, to mamy:

|AB|
	=r ⇒ |AB|=2r − jest średnicą okręgu, zauważ tam wszędzie trójkąty równoboczne i mamy:
2

	4√3		22√3
x=		=2√3 ∧ P=3*		=3√3
	2		4

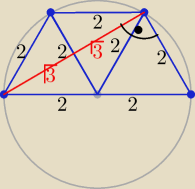blabla: Taki trapez składa się z trzech trójkątów równobocznych o boku 2

	22√3
P= 3*		=........= 3√3
	4

d= 2hΔ = 2√3

blabla:

chichi:

Cerg: Heh − też mi wyszło P=3√3 a przekątna 2√3 Ale książka mówi co innego, wiec chyba błąd w odpowiedziach po prostu.

Kuba: Tak, musi być błąd w odpowiedziach (Kiełbasa). Dobrze wiedzieć, że nie zgłupiałem