 Cześć,
mam takie zadanie:
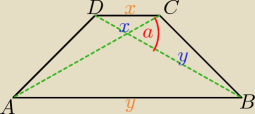
Dany jest trapez równoramienny ABCD o kącie ostrym między przekątnymi α i stosunk długości
podstaw 1:3. Oblicz pole i obwód trapezu, jeżli wiadomo, że długość przekątnej jest równa 12.
Zacząlem tak:
Przekątna x i y:
x+y = 12 { x + y = 12
{ y = 3x
Cześć,
mam takie zadanie:
Dany jest trapez równoramienny ABCD o kącie ostrym między przekątnymi α i stosunk długości
podstaw 1:3. Oblicz pole i obwód trapezu, jeżli wiadomo, że długość przekątnej jest równa 12.
Zacząlem tak:
Przekątna x i y:
x+y = 12 { x + y = 12
{ y = 3x
| x | 1 | ||
= | x + 3x = 12 | ||
| y | 3 |

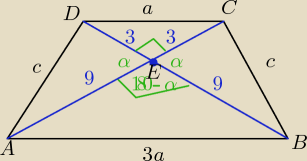 podział przekątnej jest też w stosunku 1:3
więc x+3x = 12 => x =3
IBFI= 9 IDEI= 3
teraz c wyznacz ze wzoru cosinusów z ΔBEC
a ze wzoru cosinusów z ΔCED
jeżzeli nie masz konkretnej wartosci kąta α
to odpowiedź musi być podana za pomocą kąta α
Pole trapezu:
2PΔBEC + PΔABE + PΔDCE
PΔBEC= 12* 3*9*sinα
PΔABE= 12*9*9*sinα ,, bo sin(180o−α)=sinα
PΔDEC= 12*3*3*sinα
P.S. Ja tu nie widzę innych możliwości co do rozwiązania tego zadania ,
Masz jakąś odpowiedź ?
podział przekątnej jest też w stosunku 1:3
więc x+3x = 12 => x =3
IBFI= 9 IDEI= 3
teraz c wyznacz ze wzoru cosinusów z ΔBEC
a ze wzoru cosinusów z ΔCED
jeżzeli nie masz konkretnej wartosci kąta α
to odpowiedź musi być podana za pomocą kąta α
Pole trapezu:
2PΔBEC + PΔABE + PΔDCE
PΔBEC= 12* 3*9*sinα
PΔABE= 12*9*9*sinα ,, bo sin(180o−α)=sinα
PΔDEC= 12*3*3*sinα
P.S. Ja tu nie widzę innych możliwości co do rozwiązania tego zadania ,
Masz jakąś odpowiedź ?

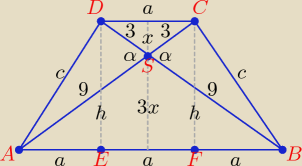 Z podobieństwa trójkątów ABS i CDS o skali podobieństwa k = 3 otrzymamy:
|AS| = |BS| = 9, |CS| = |DS| = 3
Kąty ASD i BSC mają miary α, kąty ASB i CSD miaja miary 180o−α.
Z podobieństwa trójkątów ABS i CDS o skali podobieństwa k = 3 otrzymamy:
|AS| = |BS| = 9, |CS| = |DS| = 3
Kąty ASD i BSC mają miary α, kąty ASB i CSD miaja miary 180o−α.
| 1 | 9 | |||
Pole trójkąta CDS: P1 = | *3*3*sin(180o−α) = | sinα. | ||
| 2 | 2 |
| 9 | 81 | |||
Pole trójkąta ABS: P2 = k2*P1 = 9 * | sinα = | sinα | ||
| 2 | 2 |
| 1 | 27 | |||
pole trójkąta ASD i BSC: P3 = | * 9 * 3 * sinα = | sinα | ||
| 2 | 2 |
