.
xyz: Witam, pomoże ktoś określić granice całkowania. Mam obliczyć objętość bryły ograniczzonej
z=4−x−y, z=0, y=x2, y=1
11 kwi 23:31
HGH: Powinno pomoc sporządzenie odpowiedniego rysunku, sproboj
12 kwi 01:34
piotr: | | 68 | |
∫−11∫x21∫04−x−y dz dy dx = |
| |
| | 15 | |
12 kwi 08:31
jc: W klinie
0 ≤ z ≤ 4−x−y
znajdziemy dwa ograniczone obszary
x2 ≤ y ≤ 1
oraz
1 ≤ y ≤ x2, y ≤ 4−x
Jak uzasadnić wybór pierwszego obszaru?
12 kwi 09:05
jc: A co z obszarem: 0≤z≤4−x−y, y2≤4−x, y ≥ 1?
12 kwi 12:40
xyz: Po narysowaniu wykresów tej funkcji, to −1≤x≤1 z góry ogranicza tą bryłę płaszczyzna z=4−x−y.
Pytanie jak ograniczony jest y? ∫−11{∫??4−x−y}dydx
13 kwi 19:47
luui: https://imgur.com/a/P9PfZMW
zielona prosta powstała poprzez przecięcie się dwóch płaszczyzn:
z=4−x−y oraz z=0
V =
D∭ dxdydz
Pierwszy obszar (który sobie wybrałeś/aś)
D:
−1 ≤ x ≤ 1
x
2 ≤ y ≤ 1
0 ≤ z ≤ 4−x−y
Drugi obszar
D:
x
2 ≤ y ≤ −x+4
0 ≤ z ≤ 4−x−y
Trzeci obszar
V =
D1∭dxdydz +
D2∭dxdydz
D
1:
1 ≤ y ≤ x
2
0 ≤ z ≤ 4−x−y
D
2:
1 ≤ y ≤ −x+4
0 ≤ z ≤ 4−x−y
Skoro nie ma dodatkowych ograniczeń wobec zmiennej x,
to czy istnieje czwarty obszar (połączenie 2 i 3)?
13 kwi 22:58
xyz: Kurcze, Na wykładzie nie miałem całki potrójnej, a no to mi to wygląda. Wszystkie zadania
robiłem tak jak napisałem o 19 47.
13 kwi 23:14
xyz: Pierwsze rysowalem w 3d i z wykresu odczytywałem obszary całkownia.
13 kwi 23:15
jc: xyz, dobrze robiłeś, a nawet lepiej. Całka potrójna tu nie potrzebna.
13 kwi 23:23
xyz: No i mam problem z odczytaniem obszaru po dy... Pomoże ktoś?
13 kwi 23:31
xyz: 
14 kwi 12:22
piotr:
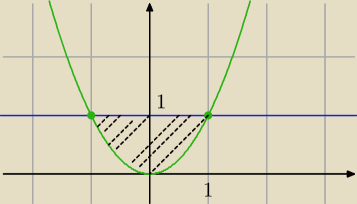
14 kwi 12:26
xyz: Czyli x2≤y≤1
14 kwi 15:40

