ostrosłup matura PR: W ostrosłupie prawidłowym czworokątnym krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem α, a kąt między sąsiednimi ścianami ma miarę β Wykaz,że cosβ(2tg²α+1)= −1

blabla: Znów ktoś, coś skasował?

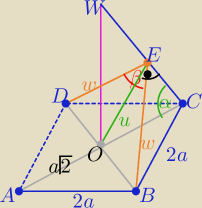
blabla: W ΔOEC : u=a√2*sinα

	a√2		1
W ΔBOE : tg(β/2)=		⇒ tg(β/2)=
	w		sinα

	1
to tg2(β/2)=
	sin2α

	2sin2(β/2)		1−cosβ
tg2(β/2)=		=
	2cos2(β/2)		1+cosβ

1		1+tg2α
	=
sin2α		tg2α

zatem

	1+tg2α		1−cosβ
		=
	tg2α		1+cosβ

po równoważnym przekształceniu ........................... mamy tezę cosβ(2tg²α+1) = −1 ================= c.n.w.

blabla: Poprawiam chochlika:

	a√2
W Δ BOE : tg(β/2)=
	u

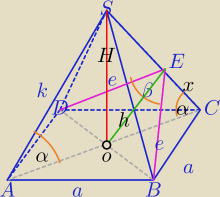Mila: BE⊥SC, DE⊥ SC, |BE|=|DE|=e, |DB|=a√2 1) W ΔDBE:

	a2
|DB|2=2e2−2e2 cosβ ⇔1−cosβ=
	e2

	h
W ΔOEC: sinα=
	0.5a√2

h=0.5a√2 sinα i x=0.5a√2cosα e²=a²(1−0.5cos²α)

	a2		1
1−cosβ=		=
	a2(1−0.5cos2α)		1−0.5cos2α)

	−cos2α
cosβ=		⇔
	2−cos2α

	−cos2α
cosβ=
	1+sin2α

=========== 3)

	1+sin2α
2tg2α+1=
	cos2α

1+sin2α
	*cosβ=−1
cos2α

==================