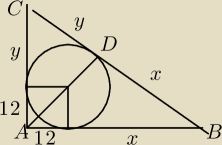 Na kole o promieniu 12cm opisano trójkąt prostokątny. Oblicz długości boków trójkąta, którego
pole jest najmniejsze
Na podstawie cechy kkk napisałem że ABC i ABD są podobne, więc skorzystałem z zależności
12+xx = y+xy+12
x(x+y) = (12 + x)( 12 + y)
x2+xy = 144+12y+12x
x2−12x−144=12y
y= 112x2−x−12
Następnie wyliczony y wstawiłem do wzoru na pole
P=(12+y)(12+x)
P= 112x3−12x
Obliczyłem pochodną
P'(x)= 14x2−12
I znalazłem x=4√3
Czy to dobry sposób?
Na kole o promieniu 12cm opisano trójkąt prostokątny. Oblicz długości boków trójkąta, którego
pole jest najmniejsze
Na podstawie cechy kkk napisałem że ABC i ABD są podobne, więc skorzystałem z zależności
12+xx = y+xy+12
x(x+y) = (12 + x)( 12 + y)
x2+xy = 144+12y+12x
x2−12x−144=12y
y= 112x2−x−12
Następnie wyliczony y wstawiłem do wzoru na pole
P=(12+y)(12+x)
P= 112x3−12x
Obliczyłem pochodną
P'(x)= 14x2−12
I znalazłem x=4√3
Czy to dobry sposób?
 Mogę prosić o pomoc?
Mogę prosić o pomoc?
| 12x+144 | ||
y = | ||
| x−12 |
| 1 | ||
P = | *(12+x)*(12+y) | |
| 2 |
| 1 | 12x+144 | |||
P(x) = (6+ | x)*(12+ | ) | ||
| 2 | x−12 |
| 1 | 12(x−12)+12x+144 | |||
P(x) = (6+ | x)*( | ) | ||
| 2 | x−12 |
| 1 | 12x−144+12x+144 | |||
P(x) = (6+ | x)( | ) | ||
| 2 | x−12 |
| 24x(6+12x) | ||
P(x) = | ||
| x−12 |
| 144x+12x2 | ||
P(x) = | ||
| x−12 |
| (144+24x)(x−12)−144x−12x2 | ||
P'(x) = | ||
| (x−12)2 |
| 144x−1728+24x2−288x−144x−12x2 | ||
P'(x) = | ||
| (x−12)2 |
| 12x2−288x−1728 | ||
P'(x) = | ||
| (x−12)2 |
| 24−24√2 | ||
x1 = | = 12−12√2 | |
| 2 |
| 24+24√2 | ||
x2 = | = 12+12√2 | |
| 2 |
| 12x+144 | ||
Obliczamy y dla x = 12+12√2 ze wzoru y = | ||
| x−12 |
| 12(12+12√2)+144 | 144+144√2+144 | |||
y = | = | = | ||
| 12+12√2−12 | 12√2 |
| 12+12√2+12 | 24√2+24 | |||
= | = | = 12+12√2 | ||
| √2 | 2 |
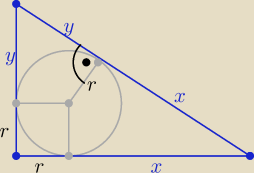 PΔ=x*y −− jest najmniejsze gdy x=y
zatem trójkąt jest prostokątny równoramienny
z tw. Pitagorasa
2(x+12)2= 4x2
(x+12)2=(√2x)2
(√2−1)x=12
x=12(√2+1)=y
a=b=12(√2+2) , c=2x= 24(√2+1)
==========================
PΔ=x*y −− jest najmniejsze gdy x=y
zatem trójkąt jest prostokątny równoramienny
z tw. Pitagorasa
2(x+12)2= 4x2
(x+12)2=(√2x)2
(√2−1)x=12
x=12(√2+1)=y
a=b=12(√2+2) , c=2x= 24(√2+1)
==========================