znajdz punkt bozena: DANE SĄ PUNKTY A(4,1) B(−2,5) I P(6,4).NA PROSTEJ RÓWNOLEGŁEJ DO PROSTEJ AB I PRZECHODZĄCEJ PRZEZ PUNKT P ZNAJDZ PUNKT RÓWNOLEGŁY OD PUNKTÓW A I B

6latek: Jednak dalej krzyczysz . Znajdz w ksiazce albo w internetach definicje punktu i zastanow sie czy punkt moze byc rownolegly do innego punktu

6latek: Moge pomoc rozwiazac to zadanie ale nie dosc ze krzyczysz z wlaczonym CAPS LOCK to przepisujesz zadanie z tym samy bledem i nawet sie tym nie zainteresujesz (chociaz masz na to zwrocona uwage)

bozena: ok rozumiem o to krzyczysz . Masz rację to ma być punkt równoodległy od punktów a i b .Nie zauważyłam błędu Proszę o pomoc

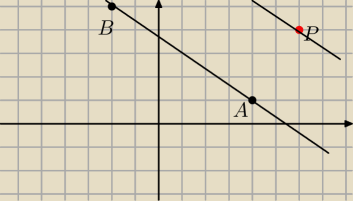
6latek: Najpierw rysunek do zadania trzeba zrobic 1) napisz rownanie prostej AB −wystarczy tez wyznaczyc jej wspolczynnik kierunkowy 2) napisz rownanie prostej rownoleglej do AB i przechodzacej przez punkt P 3) wyznacz srodek odcinka AB 4) Masz srodek odcinka AB napisz rownanie symetralnej odcinka AB 5) Wyznacz punkt przeciecia tej symetralnej i prostej przechodzacej przez punkt P Potrafisz to zrobic?

bozena: nie . wogule tego nie rozumiem .

6latek: Chwilke poczekaj

6latek: Zacznijmy od tego Rownanie prostej przechodzacej przez dany punkt R=(x₀,y₀) wyraz sie wzorem y=m(x−x₀)+y₀ ================ z tego bedzie korzystac 1) wyznaczymy wspolczynnik kierunkowy m prostej AB aby a) napisac rownanie prostej rownoleglej do prostej AB i przechodzacej przez punkt P b) napisac rownanie prostej prostopadlej do AB (rownanie symetralnej odcinka AB Mamy punkty A=(4,1) i B=(−2,5) wspolczynnik kierunkowy m prostej AB

	yb−ya		5−1		4		2
m=		=		= −		= −
	xb−xa		−2−4		6		3

	2
m1=m=−		−wspolczynnik kierunkowy prostej rownoleglej do AB
	3

	3
m2=		−wspolczynnik kierunkowy prostej prostopadlej do AB
	2

Rownanie prostej rownoleglej do AB i przechodzacej przez P=(6,4) x₀=6 y₀=4 y=m₁(x−x₀)+y₀

	2
y=−		(x−6)+4
	3

	2
y= −		x+8
	3

============ Obliczamy srodek S odcinka AB A=(4,1) B= ( −2,5) Wzory na srodek odcinka

	4+(−2)
xs=		=1
	2

	1+5
ys=		=3
	2

S=(1,3) x₀=1 y₀=3 Rownanie symetralnej odcinka AB y=m₂(x−x₀)+y₀

	3
y=		(x−1)+3
	2

	3		1
y=		x+1
	2		2

Wyznaczamy teraz ten punkt rownoodlegly o A i B

	2		3		3
−		x+8=		x+
	3		2		2

Juz sama wyznacz x i potem wstaw wyliczone x do np 1 rownania prostej i wylicz y

bozena: ok. mam nadzieje ze dam radę. DZIEKUJĘ BARDZO

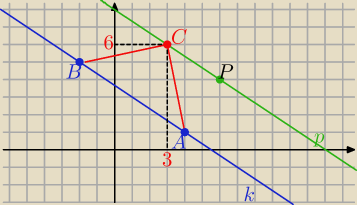
blabla: a_k= −2/3

	2
pII k to p: y= −		(x−6)+4
	3

	2		2
p: y=−		x+8 i C ∊p ⇒ C(x, −		x+8)
	3		3

|BC|=|AC| to |BC|²=|AC|² i mamy:

	2		2
(x+2)2+(3−		x)2=(x−4)2+(7−		x)2
	3		3

po uporządkowaniu i redukcji otrzymasz:

	2
x=3 to y= −		x+8= .. = 6
	3

C(3,6) =====

6latek: Także skorzystam Ciągle zapominam o tych wspolrzednych punktow

bozena: no i poległam wyliczyłam tylko x równe 3. czarna magia dla mnie .

6latek: No nie żartuj Wstawiasz np do rownania

	2
y=−		x+8
	3

	2
y=−		*3+8 (trojki skracasz )
	3

y=−2+8=6 Przemyśl tez sposob rozwiazania blabla jest krotszy od mojego

bozena: w tym problem niewiedziałam gdzie to wstawić. wszystkie zadania inne z egzaminu ogarnełam a tu pustka. dziekuje

6latek: Mozna bylo tez wstawic do tego rownania

	3		3
y=		x+		i wyjdzie to samo
	2		2

na zdrowie

bozena: zaćmienie umysłu juz mam to chyba ze względu na mój wiek hehe. za stara jestem juz chyba na szkołe ale sie nie poddaje. pozdrawiam semestr IV − 50 latka

Mila: To co jeszcze nie jest jasne?

Mila: Cześć 6−latku, w tamtym wątku dużo wpisów jest