Rachunek prawdopdobieństwa stata: Tarcza strzelecka składa się z trzech koncentrycznych kół o promieniach odpowiednio 1,2,3. Za trafienie w środkowe koło zdobywa się trzy punkty, z trafienie w kolejne pierścienie odpowiednio dwa i jeden punkt. Jakie jest prawdopodobieństwo uzyskania co najmniej trzech punktów w dwóch strzałach? (Zakładamy, że każdy strzał trafia w tarczę). Wymyśliłam tyle: A − zdarzenie polegające na uzyskaniu co najmniej 3 pkt w dwóch strzałach A' − zdarzenie polegające na uzyskaniu 0 pkt, 1 pkt lub 2 pkt w dwóch strzałach Więc P(A) = 1 − P(A') Ale nie wiem w ogóle jak wyznaczyć chociaż by moc omegi. Będę wdzięczna za pomoc

ite: Pomysł na zastosowanie zdarzenia przeciwnego jest dobry. Ale zauważ, że: 1/ Zakładamy, że każdy strzał trafia w tarczę. 2/ Za trafienie w środkowe koło zdobywa się trzy punkty, z trafienie w kolejne pierścienie odpowiednio dwa i jeden punkt. Ile najmniej punktów można uzyskać w wymaganych w zadaniu dwóch strzałach? Czy podana jest informacja, że prawdopodobieństwo trafienia w konkretny krąg zależy tylko od jego powierzchni?

stata: Najmniej można trafić dwa punkty. Trafić dwa razy w najbardziej zewnętrzne okręgi. Nie ma żadnych innych informacji, przepisałam całe zadanie.

ite: Czyli jedyna sytuacja, kiedy się nie zdobywa trzech lub więcej pkt, to trafienie z 17:56. Trzeba obliczyć stosunek pola zewnętrznego kręgu do całej tarczy i dalej pr−stwo trafienia tylko w nie. A potem już zdarzenie przeciwne.

stata: Stosunek ostatniego pierścienia do całego pola to 5/9. Prawdopodobieństwo trafienia tylko w to pole w dwóch rzutach to będzie 5/9 * 5/9? Czyli ten stosunek pól to pojedyncze prawdopodobieństwo trafienia w pole z 1 pkt, dobrze rozumiem?

ite: Policzone dobrze, a stosunek pól powierzchni decyduje o prawdopodobieństwie trafienia za 1 pkt. (jeśli pr−stwo trafienia w każdy punkt tarczy jest jednakowe).

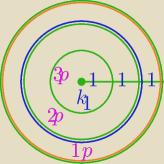
Mila: P_tarczy=9π P_k1=π P_pś=4π−π=3π− pole pierścienia środkowego P_pz=9π−4π=5π A− uzyskano co najmniej 3 punkty w 2 strzałach A' − mniej niż 3 punkty , czyli trafiono 2 razy w zewnętrzny pierścień

	5		5		25
P(A')=		*		=
	9		9		81

	56
P(A)=
	81