Równanie okręgu, proste prostopadłe, symetralne, P81: Witam, mam takie pytanie, jeśli mamy wyznaczyć równanie okręgu stycznego do jakiejś prostej "m"" w punkcie A oraz przechodzącego przez punkt B, to można wyznaczyć prostą prostopadłą np "c" przechodząca przez punkt A oraz symetralną odcinka AB i punkt przecięcia się tych prostych wyznacza współrzędne środka okręgu, ale mam takie pytanie − równanie symetralnej odcinka AB można obliczyć a) wyznaczając równanie prostej AB a potem szukamy prostej prostopadłej do odcinka AB i przechodzącej przez jego środek ( To jest pierwszy sposób ) b) Natomiast drugi to że piszemy równanie: odległość środka od punktu A jest równa odległości środka od punktu B ( bo szukamy prostej równoodległej od tych punktów ) i otrzymamy to same równanie symetralnej, bo po podstawieniu tego wyniku do równania wyjściowego otrzymamy x ∊ R I tak samo można zrobić z wyznaczaniem prostej prostopadłej "c" do stycznej "m" w punkcie A a) Albo robimy to z informacji że a*a_stycznej = −1 i w taki sposób wyznaczamy równanie tej prostej prostopadłej b) albo można to zrobić na drugi sposób równaniem: odległość środka od punktu A jest równa odległości środka od prostej do której jest styczny ( prostej m ) i tutaj moje pytanie ***dlaczego otrzymujemy najpierw dwie proste równoległe do szukanej prostej prostopadłej "c" i dopiero jak znajdziemy pomiędzy nimi prostą równoległą równo od nich oddaloną to jest ona jest tą prostą prostopadłą "c"? *** I wtedy też po podstawieniu wyjdzie x ∊ R, więc wszystko Chodzi mi po prostu o to, dlaczego stąd trzeba znaleźć prostą równoległą do tych dwóch (z równania: odległość środka od punktu A jest równa odległości środka od prostej ) i równoodległą od nich i dopiero ona Jest tą prostą prostopadłą? Bo potem to już wiem jak dalej liczyć, żeby wyznaczyć równanie okręgu 1) sposób na wyznaczenie równania okręgu to punkt przecięcia się symetralnej i prostej prostopadłej "c" do stycznej tak jak pisałem na początku 2) lub też można mając samo równanie symetralnej ułożyć równanie że odległość środka ( który leży na tej symetralnej ) od punktu A / punktu B jest równa odległości środka od prostej stycznej m ( nie można dać że |SA| = |SB| bo stąd wyznaczaliśmy to równanie symetralnej w drugim sposobie ( podpunkt b) wyżej ^^^ 3) albo bez wyznaczania symetralnej − mając tylko tą prostą prostopadłą "c" to można ułożyć kolejne równanie że odległość środka ( który leży na tej prostej c ) od punktu B jest równa odległości środka od punktu A/ prostej m ( tutaj właśnie nie można dać równania że odległość środka od A = odległości środka od prostej stycznej bo stąd wyznaczaliśmy równanie tej prostej ( kilka linijek wyżej w podpunkcie b) gdzie właśnie wyszły te dwie proste równoległe i właśnie nie wiem dlaczego akurat prosta pomiędzy nimi była tą prostą prostopadłą "c" − więc wyjdzie x ∊ R ) I z każdego z tych sposobów wyjdzie ten sam środek, tylko nie rozumiem dlaczego tam w podpunkcie b) ( na początku mojego wpisu ) prostą prostopadłą "c" do prostej m jest prosta równoodległa od tych dwóch prostych ( mam nadzieję że nie pomieszałem ) jeszcze macie ilustrację tego na kalkulatorze graficznym dla dowolnych prostych i punktów https://www.desmos.com/calculator/1thvattr7k

Maciess: Ja nie wiem co dokładnie jest tutaj pytaniem, ale podbije ci temat. Może jakiś świeższy umysł zrozumie. "i tutaj moje pytanie ***dlaczego otrzymujemy najpierw dwie proste równoległe do szukanej prostej" Bo ty w ten sposób nie szukasz prostopadłej do m przechodzącej przez A. Robisz dokładnie to co napisałeś. Czyli szukasz punktów równoodległych od B i prostej m. A taki warunek spełniają dwie proste.

Mila: Ja nie bardzo rozumiem po co tyle kombinacji. Zadanie jest proste, o ile dobrze się domyśliłam treści.

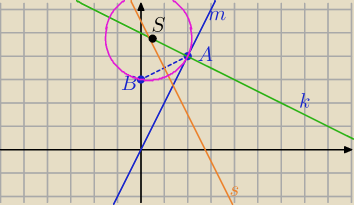
Mila: 1) AB− cięciwa

	1
k: y=−		x+5 − prostopadła do prostej m: y=2x
	2

k⊥m i A∊k 2) symetralna AB:

	11
s: y=−2x+
	2

Punkt przecięcia prostych s i k

	1		11
−		x+5=−2x+
	2		2

	1		29
S=(		,		)− środek okręgu stycznego do prostej w punkcie A
	3		6

i przechodzącego przez punkt B

	1		29		125
r2=(		)2+(3−		)2=
	3		6		36

	1		29		125
(x−		)2+(y−		)2=
	3		6		36

P81: Chodzi mi o to, że np jeśli wyznaczamy symetralną AB to można to zrobić układając równanie że odległość środka od A = odległości środka od B i stąd otrzymujemy równanie symetralnej i potem chcąc wyznaczyć równania okręgów nie można z powrotem do tego równania podstawić bo z tego wyznaczaliśmy, więc trzeba ułożyć równanie np odległość środka od A/ lub od B jest równa odległości środka od prostej No i tak samo z równaniem prostej prostopadłej np k, jeśli ją wyznaczymy z faktu że a_k*a_m = −1 i potem byśmy podstawili do równania że odległość środka od A ( który leży na prostej m ) jest równa odległości środka od prostej to też wyjdzie x € R czyli wniosek wygląda tak jakbyśmy wyznaczali stąd to równanie ( Tej prostopadłej k) ( czyli tak samo jak z wyznaczeniem symetralnej AB ( np jako prostą prostopadłą przechodząca przez środek odcinka AB ) jak podstawimy ją potem do równania SA = SB to mamy x € R czyli Że z tego równania można ją wyznaczyć ) i tutaj moje pytanie/ problem − skoro tak jest, no to spróbowałem z tego równania od początku wyznaczyć to równanie symetralnej ( skoro ona spełnia to równanie ) ( tak samo jak z symetralną i równaniem odległ. Środka od A = odległości środka od B ) Tylko że jak napisałem to równanie ( SA = odległości środka od prostej m ) to mi wyszły dwie proste równoległe które są prostopadle do m, no i dopiero prosta, która leży idealnie pomiędzy nimi ( i też jest do nich równoległa ) jest tą szukaną prostą prostopadłą do "m" czyli prosta k W skrócie mam na myśli to, że dlaczego akurat prosta równoległa i idealnie leżąca pomiędzy tymi dwoma z równania SA = odległości środka od prostej m, Tzn chcę się dowiedzieć dlaczego po wyznaczeniu prostej prostopadłej do m, żeby dalej zrobić takie zadanie to nie można wstawić do równania SA = odległości środka od prostej ( bo stąd się niby wyznacza to równanie jako prostą równoległą pomiędzy tymi dwoma z równania ) tylko trzeba wstawić do równania np takiego SB = odległości od prostej m lub SB = SA