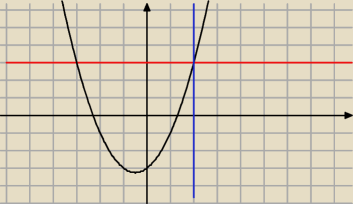
 Dane sa dwie funkcje y=f(x) oraz y1=g(x) ,obie okreslone w tej samej dziedzinie D
Sformuluj warunek konieczny i dostateczny na to aby
a) wykresy tych funkcji były symetryczne wzgledem prostej o rownani y=k
b)wykresy tych funkcji byly symetryczne wzgledem prostej o rownaniu x=p
c) podaj wzor funkcji ktorej wykres jest symetryczny do wykresu funkcji o rownaniu y=x2+x−3
1) wzgledem prostej y=3
2) wzgledem prostej x=2
jeśli będe miał a i b to co zrobie
Dane sa dwie funkcje y=f(x) oraz y1=g(x) ,obie okreslone w tej samej dziedzinie D
Sformuluj warunek konieczny i dostateczny na to aby
a) wykresy tych funkcji były symetryczne wzgledem prostej o rownani y=k
b)wykresy tych funkcji byly symetryczne wzgledem prostej o rownaniu x=p
c) podaj wzor funkcji ktorej wykres jest symetryczny do wykresu funkcji o rownaniu y=x2+x−3
1) wzgledem prostej y=3
2) wzgledem prostej x=2
jeśli będe miał a i b to co zrobie
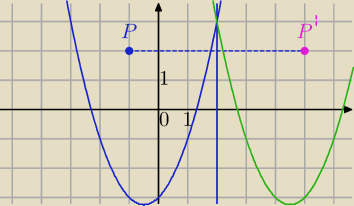 b)wykresy funkcji symetryczne względem prostej o równaniu x=p
1)
Symetria względem prostej x=p
P(x,y) − punkt płaszczyzny
P'(x',y') − punkt symetryczny do P względem prostej x=p
a) y'=y
S=(p,y) − środek odcinka PP'
b)wykresy funkcji symetryczne względem prostej o równaniu x=p
1)
Symetria względem prostej x=p
P(x,y) − punkt płaszczyzny
P'(x',y') − punkt symetryczny do P względem prostej x=p
a) y'=y
S=(p,y) − środek odcinka PP'
| x+x' | y+y' | |||
p= | i y= | |||
| 2 | 2 |



 Pozdrawiam.
Pozdrawiam.


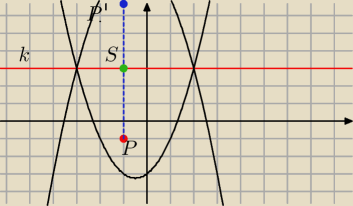 Musimy rozpatrzyc symetrie wzgledm prostej y=k
Punkt P =(x,y) takie ma wspolrzedne
Punkt P' =(x',y') jest to punkt symetryczny do punktu P
Tutaj mamy x'=x
Srodek S odcinka PP' to S=(x,k)
Musimy rozpatrzyc symetrie wzgledm prostej y=k
Punkt P =(x,y) takie ma wspolrzedne
Punkt P' =(x',y') jest to punkt symetryczny do punktu P
Tutaj mamy x'=x
Srodek S odcinka PP' to S=(x,k)
| x+x' | y+y' | |||
x= | i k= | |||
| 2 | 2 |

 Pozdrawiam
Juz dzisiaj jest troche lepiej ,Pije herbatki
Pozdrawiam
Juz dzisiaj jest troche lepiej ,Pije herbatki 
 super.
super.