geometria analityczna kun: Dane są współrzędne wierzchołków A(−3,−2) i C(2,8) trapezu ABCD. Oblicz współrzędne punktu przecięcia przekątnych tego trapezu, jeżeli podstawa AB jest cztery razy dłuższa od podstawy DC. wynik ma wyjść S(1,6) Jak to zrobić na wektorach? Bo zrobiłem bez wektorów ale jestem średnio przekonany do tego rozwiązania.

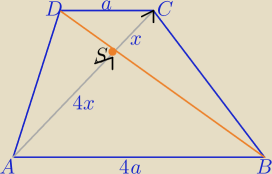
blabla: Z podobieństwa trójkątów ABS i DCS w skali k=4 → → AS=4 SC [x+3,y+2]= 4[2−x, 8−y] x+3=8−4x i y+2=32−4y x=1 y=6 S(1,6)

kun: dziękuję

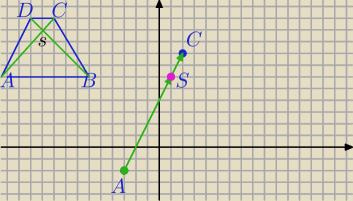
Mila: A(−3,−2) i C(2,8)

	1
ΔDSC∼ΔABS w skali k=		⇔
	4

S=(x,y)− punkt przecięcia przekątnych

SC		1
	=
AS		4

	1
SC→=		AS→
	4

	1
[2−x,8−y]=		[x+3,y+2]
	4

[8−4x,32−4y]=[x+3,y+2] x+3=8−4x y+2=32−4y 5x=5, x=1 5y=30 y=6 S=(1,6)

blabla:

Get it back: Mozna poprosić o rozwiązanie bez wektorów ?

chichi: A=(−3, −2) C=(2, 8)

	−3+4*2		−2+4*8
S=(		,		)=(1,6) i po ptokach
	5		5

Get it back: NIc z tego nie rozumiem

blabla:

blabla: Podział odcinka punktem S w stosunku k=4

	xA+k*xC		yA+k*yC
xS=		i yS=
	k+1		k+1

....................................

chichi: A=(x_A, y_A) S=(x_S, y_S) B=(x_B, y_B)

	xA+k*xB		yA+k*yB		|AS|
S=(		,		), gdzie k=
	1+k		1+k		|SB|

blabla: @Get 100 razy pisałeś tę zależność

blabla:

chichi:

Get it back: Już kojarzę . dziękuje , Pozdrawiam .