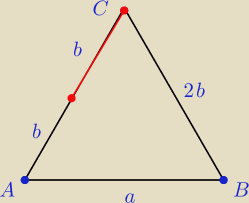
Problem, trójkąt Szkolniak: Oblicz długość podstawy trójkąta równoramiennego ABC wiedząc, że jego ramię ma długość 16 i że odległość środka ramienia od przeciwległego wierzchołka podstawy wynosi 12. Nie wiem czy ja kompletnie źle rozumiem to zadanie, ale czy z tego nie wynika że to jest ta długość którą zaznaczyłem na rysunku na czerwono?

ite: od przeciwległego wierzchołka podstawy → chodzi o B

Szkolniak: Właśnie coś mi kompletnie nie pasowało.. Czy dla Ciebie jest to również dziwnie sformułowane i powinno być inaczej, czy to po prostu ja coś pokręciłem?

Maciess: 'ta' to znaczy która? 'odległość środka ramienia od przeciwległego wierzchołka podstawy wynosi 12' Wydaje mi się, że to nie czerwony odcinek, tylko od czerwonego punkciku do wierzchołka B.

Maciess: W sumie wydaje mi się, że jest zrozumiale napisane i ciężko to inaczej interpretować.

ite: Podstawą tego trójkąta jest odcinek AB, wierzchołkiem leżącym naprzeciw boku AC jest B. Pewnie zasugerowałeś się tym środkiem ramienia, ale opis jest jasny.

Szkolniak: W sumie zawsze mało robiłem tych zadań z geometrii i ostatnio przysiadłem żeby ich zrobić sporo więcej, więc może po prostu wynika to z mojego małego obycia z tym tematem i źle zinterpretowałem Chociaż tak naprawdę jeśli się zaznaczy ten środek odcinka AC i pomyśli, to jedyny logiczny odcinek będzie właśnie do wierzchołka B

chichi: Trójkąt równoramienny jak sama nazwa mówi ma dwa ramiona równej długości, zatem jeśli rozpatrujemy punkt będący środkiem ramienia AC, to przeciwległym wierzchołkiem podstawy do AC jest B i analogicznie jeżeli rozpatrujemy ramię BC, to jest to ramie leżące naprzeciwko A

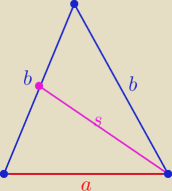
blabla: Ze wzoru na długość środkowej w trójkącie

	1
s=		√2b2+2a2−b2
	2

144*4= 2a²+256 a²=160 , a>0 a=4√10 ======== i po ptokach

Mila: II sposób 2 razy tw. cosinusów.

blabla:

chichi: @Mila 2 razy tw. Carnota to wyprowadzenie tego wzoru,z którego korzysta @Eta pozdrawiam

blabla: @chichi A gdzie tu widzisz Etę ?

chichi: @Eta przejęzyczenie