Dowód planitetria mis: Dany jest trójkąt ABC. Na półprostej AB wyznaczamy punkt A1, taki że |AA1| = 4|AB|, na półprostej BC wyznaczamy punkt B1, taki że |BB1| = 3|BC|, na półprostej CA wyznaczamy punkt C1, taki że |CC1| = 2|CA|. Uzasadnij, że pole trójkąta A1B1C1 jest 18 razy większe od pola trójkąta ABC. próbowałem szukać jakiś wspólnych wysokości ale chyba nici z tego, prosiłbym pomoc

Sampas :

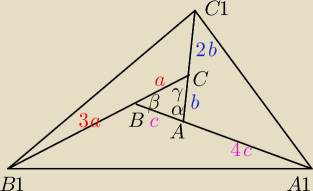
	1		1		1
PABC=		absinγ=		acsinβ=		bcsinα
	2		2		2

∡B1CC1=180−γ

	1		1
PB1CC1=		4a*2b*sin(180−γ)=		absinγ*8=8PABC
	2		2

i analogicznie z kolejnymi trójkątami, tylko mi wychodzi P_A1B1C1=36P{ABC}

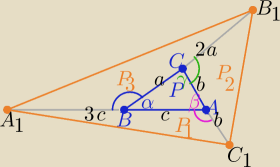
a@b: Na półprostej AB ( a u Ciebie na BA) 2P(ABC)=acsinα=bcsinβ=absinγ 2P₁=4bc sinβ=4P 2P₂=4absinγ=4P 2P₃=9acsinα=9P P(A₁B₁C₁)= 17P+P P(A₁B₁C₁)=18P ================

mis: Dziękuję wszystkim za pomoc