uklad rownan qTarantin0: Rozwiąż układ równań. x²+y²=10 y=|x−1|−3 czy mogę wyrażenie y² podstawiając ten y liczyć jako wzór skróconego mnożenia (a−b)² gdzie a=|x−1|? Bo wyszło mi x1=1 y1=−3 x2=3 y2=−1 a powinno być jeszcze jedno rozwiązanie x3=−3 y3=1 jak to zrobić żeby wyszły te 3 rozwiązania?

wredulus_pospolitus: x²+y² = 10 <−−− to byc równanie okręgu

qTarantin0: to znaczy? bo utknąłem, nie wiem jak poprawnie zrobić to zadanie

wredulus_pospolitus: a pokaż jak liczyłeś po podstawieniu

qTarantin0: x²+(x²−2x+1)−6x+6+9=10 x²−4x+3=0 Δ=4 x1=1 x2=3

wredulus_pospolitus: a czemu po podstawieniu 'zniknięty' został moduł

wredulus_pospolitus: x² + (x−1)² − 6*|x−1| + 9 = 0 <−−− tak powinno być

wredulus_pospolitus: oczywiście .... = 10 miało być

Get it back: y²=(|x−1|−3)²= (x−1)²−2*3*|x−1|+9=(x−1)²−6|x−1|+9 wedlug mnie tak powinno byc

wredulus_pospolitus: no i teraz pojawi Ci się to dodatkowe rozwiązanie dla przedziału x<1 które wcześniej pomijałeś

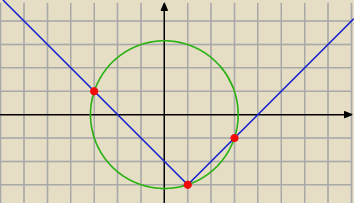
Qulka: odp: x=−3 lub x=1 lub x=3

qTarantin0: czyli dla x≥0 ...−6x+6 a dla x<0 ...6x−6 i wtedy trzecie rozwiązanie to x=−3 tak?

wredulus_pospolitus: nie ... dla x≥1 −6x+6 dla x<1 6x−6

Get it back: Nie dla x≥0 i x<0 bo nie masz |x| Tylko masz |x−1| wiec liczysz dla x≥1 wtedy |x−1|=x−1 oraz dla x<1 wtedy |x−1|= −(x−1)= −x+1=1−x

qTarantin0: Ok, wszystko rozumiem dzięki wam, bardzo dziękuję

Filip: czesc wreduluspospolitus.