Oblicz p(a-b). szymon: Zdarzenia A,B ⊂Ω są jednakowo prawdopodobne, zajście przynajmniej jednego z nich jest zdarzeniem pewnym, a p(a＼b)=2/3. Oblicz p(a−b). Skoro zdarzenia są jednakowo prawdopodobne i przynajmniej jedno z nich jest zdarzeniem pewnym to znaczy że albo p(a) albo p(b) jest rowne 1 lub oba są tyle równe? bo może wyjść p(a) i p(b)= na przykład 1/2 ale wtedy żaden z nich nie jest zdarzeniem pewnym. Bardzo prosze o pomoc

wredulus_pospolitus: nie ... tu nie jest napisane, że 'przynajmniej jedno z nich jest zdarzeniem pewnym' tylko że ZAJŚCIE przynajmniej jednego z nich jest zdarzeniem pewnym, czyli: P(AuB) = 1 Przepraszam bardzo ale co oznacza P(A\B) oraz P(A−B) ? Bo wedle mych oznaczeń pierwsze oznacza 'zaszło A, ale nie zaszło B' a drugie jest bezsensu

szymon: Szczerze mówiąc to nie widzę różnicy w tym że przynajmniej jedno z nich jest zdarzeniem pewnym w odniesieniu do tego co napisałeś. Te P(a−b) itd to juz bez znaczenia bo zalezy mi na zrozumieniu całego tego zdania. Mógłbym prosić o szczegółowe rozpisanie bo zastanawiam się nad tym już tyle czasu..

Maciess: No nie ruszysz dalej jak nie zrozumiesz tego co ci napisał wredulus.

szymon: Zależy mi tylko na szczegółowym wyjaśnieniu tego co napisał wredulus bo kompletnie tego nie łapie. Jak sie ma to "zajście przynajmniej jednego z n ich jest zdarzeniem pewnym" do tego że te zdarzenia są jednakowo prawdopodobne. Dla mnie to się wyklucxa ale napewno tak nie jest dlatego bardzo chciałbym to zrozumieć.

a@b:

	2
P(A|B)=		−−− prawd. warunkowe
	3

P(A−B)= ? z treści zadania P(A)=P(B) i P(AUB)=1 i P(AUB)= P(A)+P(B)−P(A∩B) to 1= 2P(B)−P(A∩B) ⇒P(A∩B)= 2P(B)−1

	P(A∩B)
P(A|B)=
	P(B)

2		2P(B)−1		3
	=		⇒ P(B)=		= P(A)
3		P(B)		4

zatem: P(A−B)= P(A)−P(A∩B)

	1
P(A−B)=
	4

==========

a@b: Dla jasności

	6		1
P(A∩B)=2P(B)−1=		−1=
	4		2

	3		1		1
P(A−B)=		−		=
	4		2		4

szymon: Zależało mi na interpretacji tego co wyżej napisałem i dlaczego P(A∪B)=1 Tak jak wspomniałem skoro zdarzenia są jednakowo prawdopodobne to znaczy że mogą mieć prawdopodobieństwo 1/2 lub 3/4. przy czym dalej jest napisane że zajście przynajmn iej jednego z nich jest zdarzeniem pewnym a zdarzenie pewne to cała omega i mi się w tym moemencie to wyklucza. Nie wiem czy ktokolwiek rozumie o co mi chodzi

a@b: I jak szymon? jasne?

wredulus_pospolitus: Szymon "prawdopodobieństwo zajścia PRZYNAJMNIEJ jednego z nich jest pewne" oznacza tyle co: na pewno mamy sytuację taką, że zajdzie A LUB B Na przykładzie: zdarzenie L −−− jutro wstaniesz lewą nogą zdarzenie R −−− jutro wstaniesz prawą nogą możemy powiedzieć, że (o ile będziesz żył) to prawdopodobieństwo zajścia przynajmniej jednego z tych zdarzeń jest pewne. Ale to nie oznacza, że P(L) = 1 = P(R) ... oznacza tylko że przynajmniej jedno z nich MUSI zajść i stąd P(L u R) = 1

szymon: Dobra do tej pory rozumiem, natomiast skoro jest napisane że zdarzenia a i b są jednakowo prawdopodobne to tak jak wyszło w rozwiązaniu p(b)=p(a)=3/4, a w tym co werdelus napisałeś "oznacza tyle co: na pewno mamy sytuacje taka ze zajdzie a lub b". a w obliczeniach wyszło ze a i b rowna sie 3/4 i nad tym sie tylko zastanawiam czemu tak jest

wredulus_pospolitus: nie rozumiem Twojego pytania/zastanawiania się

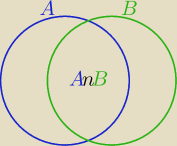
a@b: P(AUB)=P(A)+P(B)−P(A∩B)

wredulus_pospolitus: jeszcze raz wrócę do przykładu który podałem istnieje jakieś prawdopodobieństwo że jutro wstanie lewą nogą, a jakieś że prawą nogą ... ale to nie oznacza że nie możesz wstać OBIEMA jednocześnie.

	3		3
Stąd też możliwe jest że będzie P(L) =		P(R) =
	4		4

Co oznacza, że w 25% przypadków wstajesz lewą pierwszą, 25% prawą pierwszą, a w 50% obiema jednocześnie

szymon: Okey już rozumiem dziękuję