trójkąt mat-fiz: W trójkącie ABC o bokach AB=4, AC=2 , BC=3 Z wierzchołka A poprowadzono dwusieczną , która przecięła bok BC w punkcie D Przez punkt C poprowadzono prostą równoległą do boku AB, która przecięła prostą AD w punkcie E Wyznacz długość odcinka DE

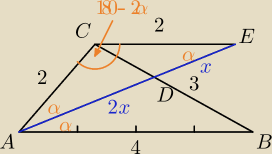
Saizou : ΔABD ~ΔCED (kkk), zatem |AD| = 2x Z tw, sinusów w ΔACE mamy

3x		2
	=
sin(180−2α		sinα

2sin(2α) = 3x*sinα 2*2sinαcosα = 3x*sinα

	4cosα
x =
	3

Z tw. cosinusów w ΔABC mamy 3² = 2² + 4² −2*2*4*cos(2α)

	11
cos(2α) =
	16

	11
cos2α−1 =
	16

	3√3
cosα =		(α−kąt ostry), zatem
	4

x = √3

Szkolniak:

	√6
Mi wyszło x=
	2

Saizou : bo u mnie jest błąd obliczeniowy

	11
2cos2α−1 =
	16

	3√6
cosα =
	8

	√6
x =
	2

Szkolniak: O, super, dobrze mi wyszło ja z kolei skorzystałem z twierdzenia o dwusiecznej, a następnie z cosinusów w trójkącie ABD i ADC.

Saizou : Zwyczajem Ety