planimetria Marcin: Na okręgu opisano trapez prostokątny ABCD. Odległości środka okręgu od końców dłuższego z ramion wynoszą odpowiednio a i 2a. Wykaż, że pole trapezu wynosi 18a² /5

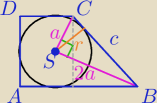
chichi: Z ΔCSB: a²+(2a)²=c² ⇒ c=√5a

	1		1		r√5a		2√5a
P=		*a*2a=a2 ∧ P=		*r*√5a ⇒ a2=		⇒ r=
	2		2		2		5

	1		2√5a		4√5a		18a2
PABCD=		*		*2(		+√5a)=		□
	2		5		5		5

Marcin: Skąd we wzorze na pole trapezu długość ramienia c? Zupełnie nie rozumiem

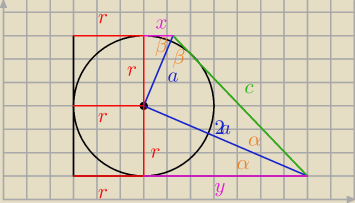
Saizou : Oblicz x oraz y z Pitagorasa

chichi: @Marcin z warunku opisywalności czworokąta na okręgu mamy, że |AD|+|BC|=|AB|+|CD| i ze

	1		1
wzoru na pole czworokąta opisanego na okręgu P=		r(a+b+c+d) mam P=		r*2*(|AD|+|BC|)
	2		2

	4√5a
u mnie |AD|=2r=		i |BC|=c=√5a, czy teraz rozumiesz?
	2

Saizou : Albo patrząc na mój rysunek widać, że x+y=c (z stycznych do okręgu)

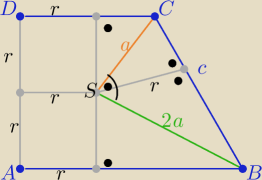
blabla: P(trapezu)= 2r²+2P(ΔBCS) = 2r²+2a²

	a*2a		4
c2=5a2 i r=		to r2=		a2
	c		5

	8
P=		a2+2a2
	5

	18
P=		a2
	5

==========