Udowodnij, że dla każdej liczby rzeczywistej m równanie mx2 − (1 − m)x − m = 0 m kasztan: Udowodnij, że dla każdej liczby rzeczywistej m równanie mx² − (1 − m)x − m = 0 ma co najmniej jedno rozwiązanie. Może ktoś pomóc ?

Jerzy: Wykaż,że Δ ≥ 0 dla każdego m.

Saizou : I przypadek m =0 daje równanie liniowe. II przypadek m≠0 daje równanie kwadratowe, które ma co najmniej jedno rozwiązanie, gdy Δ ≥ 0

Filip: dla m=0 mamy jedno rozwiqzanie, a maja hyc conajmniej jedno

kasztan: znaczy zrobiłem to tak i wyszło żę m=0 albo 5m²−2m+1>=0 czyli delta ujemna więc neiskończenie wiele rozwiązań. I to już jest wszystko ? Czyli m=0 lub m należy do R czyli ma co najmniej 1 rozwiązanie.

I'm back: kasztan ... co "5m²−2m+1>=0 czyli delta ujemna więc neiskończenie wiele rozwiązań" 1. 5m²−2m+1>=0 vs delta ujemna Hęęęę 2. delta ujemna vs nieskończenie wiele rozwiązań Hęęęęęę

Filip: tak, 5m²−2m+1 ma delte<0 i a>0, wiec 5m²−2m+1>=0 ma jest prawdziwe dla kazdego m∊R

I'm back: Boże ... ale on przeskok myślowy zrobił. Tak samo jak później: "Czyli m=0 lub m należy do R czyli ma co najmniej 1 rozwiązanie." ehhh

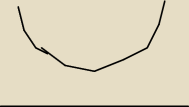
kasztan: Aaaa za szybko pisałem, jeszcze raz powoli: mam m=0 które daje mi x=0 (f.liniowa dalej liczę deltę (delta >=0) i wychodzi mi 5m²−2m+1 co oznacza że delta jest <0 ale a>0 więc wykres będzie nad osią x czyli ma nieskończenie wiele rozwiązań bo delta ma być >=0 a więc mam m=0 i m należące do R. Teraz zrozumiale jest to co napisałem ?

kasztan: I'm back sorki, na szybko to pisałem więc dlatego taki przeskok w rozwiązaniu.