Kombinatoryka i geometria Granatek: Dzień dobry, mam problem z zadaniem: Przekątne ośmiokąta wypukłego mają tę własność, że żadne trzy nie przecinają się w jednym punkcie. W ilu punktach przecinają się przekątne tego wielokąta? Kompletnie umiem sobie wyobrazić opisanej w zadaniu w sytuacji, więc nie wiem co mam liczyć :C Pomocy :C

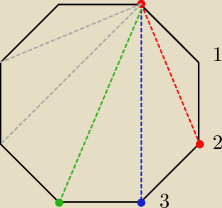
I'm back: czerwona przekątna przecina się z przekątnymi wychodzącymi z wierzchołka 1 (czyli z iloma? ile przecięć masz?) niebieska przekątna przecina się z przekątnymi wychodzącymi z wierzchołka 1 i wierzchołka 2 (czyli ile przecięć masz?) zielona przekątna przecina się z przekątnymi wychodzącymi z wierzchołka 1 i z wierzchołka 2 i z wierzchołka 3 POMIJAJĄC (ale na razie o tym zapomnij i licz wraz z nią) przekątną pomiędzy wierzchołkami 1 i 3 (czyli ile przecięć masz ?) zauważ, że pozostałe dwie szare przekątne to powtórzenie sytuacji niebieskiej i czerwonej. Więc ile będzie przecięć dla przekątnych wychodzących z tegoż wierzchołka? I jak to teraz uogólnić dla całej figury? I później jak dokonać korekty ilości ?

I'm back: jeszcze przy niebieskiej i zielonej przekątnej będą później odejmowane te przekątne z wierzchołka 2 (lub 3) które lądują w czerwonym wierzchołku lub w wierzchołku w którym rozpatrywany kolor przekątnej się 'kończy'

kerajs: 70

Granatek: No niestety, nawet jak liczę "na piechotę" to mi nie wychodzi 70 przecięć