Geometryczne Fineasz: 1) Spodki wysokości trójkąta ostrokątnego ABC łączymy odcinkami tworząc nowy trójkąt. Znaleźć długości boków tego trójkąta znając długości boków trójkąta ABC. 2) Odcinki AB i CD są średnicami okręgu, a punkt M należy do tego okręgu. Punkty P i R są rzutami prostokątnymi punktu M na proste AB i CD. Wykazać, że przy ustalonych średnicach AB i CD długość odcinka PR nie zależy od wyboru punktu M.

Fineasz: Bump

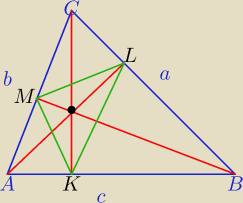
Mila: 1) W ΔAKC:

	AK
cosA=		⇔|AK|=b* cosA
	b

W ΔAMB:

	AM
cosA=		⇔|AM|=c*cosA
	c

2) W ΔAKM: z tw. cosinusów |MK|²=b²cos²A+c²cos²A−2*bc cos²A*cosA |MK|=cosA*√b²+c²−2bc cosA⇔ |MK|=a*cosA 3) Analogicznie : |KL|=b*cosB |ML|=c*cosC 4) cosinusy kątów Δ ABC możesz obliczyć z tw. cosinusów:

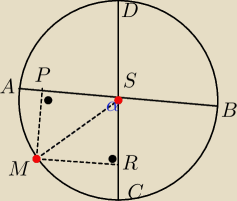
Sampas : Na czworokącie MRSP można opisać okrąg, gdyż kąty MRS i MPS są proste. Ponad to |MS|=R i jest średnicą okręgu opisanego na czworokącie MRSP.

	|PR|		1
z tw. sinusów dla trójkąta PRS wynika ,że		=2*		R
	sinα		2

zatem |PR|=Rsinα z tego wynika, że długość odcinka |PR| nie zależy od wyboru punktu M. To jest moje rozwiązanie nie jestem pewien czy o to dokładnie chodzi.

Mila: Sampas− Bardzo ładne rozwiązanie

Fineasz: Dziękuję wam za te rozwiązania. Są one w pełni przeze mnie zrozumiane.

Mila: To pięknie