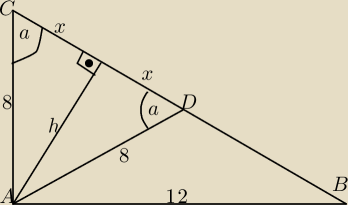
Geometria zzzz: W trójkącie prostokątnym ABC przyprostokątne AC i AB mają długość odpowiednio równą: 8 i 12. Na przeciwprostokątnej CB obrano punkt D tak, że |∠ACD|=|∠ACB|. Oblicz pole trójkąta ADC.

	12		3		h
tgα =		=		=
	8		2		x

	2
x =		h
	3

	h
sinα =
	8

	h
cosα =
	12

Korzystając z sin²α + cos²α = 1 podstawiam:

h2		h2		576		24√13
	+		= 1 ⇒ h2 =		⇒ h =
64		144		13		13

	2		24√13		16√13
x =		*		=
	3		13		13

	1		384		7
PADC =		* 2x * h =		= 29
	2		13		13

Czy ktoś mógłby stwierdzić, czy wyliczony przeze mnie wynik jest poprawny? Z góry dziękuję.

I'm back: może trochę łatwiej: |BC| = 4*√4+9 = 4*√13

	8*12		24√13
z porównania wzorów na pole ABC −> h =		=
	4√13		13

	2		2		2		242		384
x =		h −−> PACD = x*h =		h2 =		*		=
	3		3		3		13		13

więc wychodzi tyle samo

ICSP: coś te kąty na rysunku się nie zgadzają z treścią. inaczej: |BC| = 4√13

	1		1
P =		*8*12 =		*4√13*h
	2		2

24 = √13h

	24√13
h =
	13

czyli to samo co u Ciebie.

h		12
	=
x		8

	2		16√13
x =		h =
	3		13

	1		16*24*13		16*24
P =		*2x*h =		=
	2		13*13		13

chyba się zgadza.

zzzz: Ah rzeczywiście wkradła mi się mała pomyłka. Chodziło w poleceniu o |∠ADC|=|∠ACB|.

blabla: Ajjjjjjjjj

Filip: tak, zgadza sie

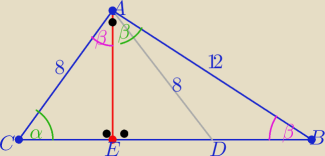blabla: Jeszcze raz np: tak P(ABC)=48 P₁=P(ACE) , P₂=P(AEB) P₁+P₂=48 Z podobieństwa trójkatów ACE i AEB z cechy (kkk)

	8		2		P1		4		4
w skali k=		=		⇒		=k2=		⇒ P1=		P2
	12		3		P2		9		9

	13		4*48
to		P1=48 ⇒ P1=
	4		13

P(ACD)=2P₁

	8*48		7
P(ACD)=		=29
	13		13

===================