tangensy Michał: W trapezie o podstawach 20 i 5 i wysokości 12 przekątne są prostopadłe Wyznacz tangensy kątów nachylenia przekatnych do dłuższej podstawy

jkl:

3		4
	i
4		3

Michał: Jak dojść do tego wyniku ?

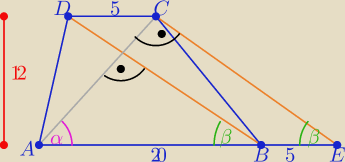blabla: Jeden ze sposobów P(ABCD)=150 = P(ΔAEC)

	1		a2		1
P(AEC)=		*		ctgα=		. ctgβ=tgα
	2		ctgα+ctgβ		tgα

	1		625		25
		+tgα=		=
	tgα		300		12

	25
tg2α−		tgα+1=0 , Δ= 49/144
	12

	25   7   − 12   12		3		25   7   + 12   12		4
tgα=		=		lub tgα=		=
	2		4		2		3

	3		4
Odp: tgα=		, tgβ=		lub odwrotnie
	4		3

=========================