proszę o rozwiązanie
anna: w trójkącie ABC bok AB ma długość c zaś kąty trójkąta przylegające do boku AB są równe α i β
Oblicz promień okręgu opisanego na tym trójkącie, jeśli
| | 2 | |
c = 8 i sin (α + β) = |
| |
| | 5 | |
2 kwi 19:36
Saizou :
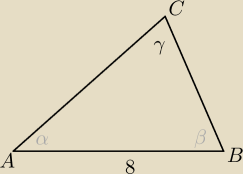
Z tw. sinusów
| | 4 | | 4 | | 4 | | 4 | |
R = |
| = |
| = |
| = |
| = 10 |
| | sinγ | | sin(180−(α+β)) | | sin(α+β) | | | |
2 kwi 20:10
Filip: zwykle podstawienie do wzorku
2 kwi 20:16
anna: dziękuję nie wiedziała co zrobić z sumą
2 kwi 21:11
anna: przepraszam ale wynik ma być 6 a nie 10
2 kwi 21:16
Saizou :
Na pewno dobre dane podałaś?
2 kwi 23:06
Filip: mhm, no tak bo
8/sinγ=2R
R=82sinγ
3 kwi 12:02
anna: wynik jest taki jak podałam , sprawdzałam chyba że w podręczniku jest błąd
3 kwi 14:23